Кроме того, целесообразно разработать и подробно исследовать последствия наиболее вероятной аварии для данного предприятия или промышленного объекта, основываясь на анализе статистических данных по происшествиям, последовательности (хронологии) их развития и заключениях экспертов.
Последовательности развития гипотетических аварий, схема которых приводится на Рис.1.2, показывают, что практически при любой крупной аварии на промышленном объекте возникает очаг загорания, обусловленный большим количеством горючих материалов, имеющихся на производстве.
Известно, что при воспламенении горючих газовых или пылегазовых смесей по ним распространяется пламя, представляющее собой супер-позицию химических реакций с выделением большого количества тепла. При детонации эти процессы происходят чрезвычайно быстро, что приводит к образованию взрывной волны; при сравнительно медленном горении большинства пылегазовых горючих смесей взрывная волна не возникает. Поэтому, несмотря на широкое распространение в литературе такого названия, взрыва как такового не возникает. Подобное ошибочное толкование горения (без детонации) газообразных и парообразных веществ связано, очевидно, с видимыми результатами этого явления, приводящего к повышению давления в помещениях и к их частичному или полному разрушению. Поэтому, если не разделять процессы горения, носящего по своим внешним проявлениям характер взрыва, и собственно разрушения оболочек, а рассматривать все явление в целом, то такую аварийную ситуацию можно считать взрывом.
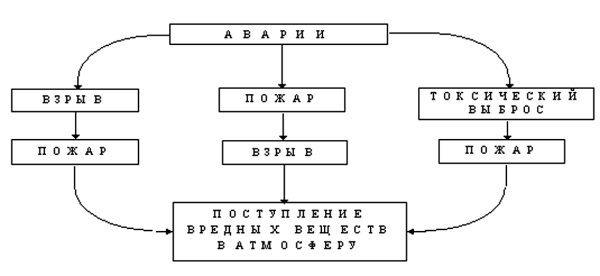
Рис.1.2. Схема хронологии развития аварий.
Таким образом, называя горючие газообразные и парообразные вещества, а также пылегазовые смеси взрывоопасными, а их горение – взрывом, следует помнить об условности этих терминов. На практике часто невозможно с полной уверенностью идентифицировать горение и взрыв, а также установить последовательность этих событий. Следует отметить, что вероятность пожара после взрыва очень велика. Реализация взрыва после пожара или пожара после выброса токсического вещества в атмосферу в заметной степени обусловлены термодинамическими характеристиками рабочих тел, их физическим состоянием, наличием доступа окислителя и т.п. В любом случае, как это следует из схемы Рис. 1.2, авария на крупном промышленном производстве приводит к выбросу в окружающую среду токсических веществ
1.3. Математическое моделирование атмосферных выбросов
В настоящее время усилиями ученых всего мира создан единый фонд моделей процессов, протекающих в живой и неживой природе. Эти модели, как правило, основываются на небольшом числе фундаментальных принципов, связывающих воедино разнообразные факты и представления естественных |наук. Каждая модель в этом фонде занимает определенное место, установлены пределы ее применимости и связь с другими моделями. Наличие такого фонда моделей придает уверенность исследователям при их использовании в практической деятельности – ведь каждая из этих моделей благодаря связям с другими моделями опирается не столько на специфическую проверку ее самой, сколько на весь практический опыт человечества. Для каждого конкретного объекта в этом фонде можно выбрать наиболее подходящую модель или модифицировать ее из близких по характеру моделей.
Применительно к задачам охраны окружающей среды развитость теорий возникновения и трансформации загрязняющих веществ в природных средах, проявившая себя в наличии грандиозного фонда природных процессов, с одной стороны, определяет высокую эффективность использования математических моделей и методов в инженерной практике, а с другой стороны – дает исследователям единую картину окружающего мира.
В целом основу конструктивного подхода к проблеме взаимодействия человека с природой дает моделирование (в частности, математическое) в сочетании с целенаправленными экспериментальными исследованиями. Загрязнение природных сред – одно из наиболее типичных проявлений такого взаимодействия.
Множество факторов, которое необходимо учитывать в моделях, находится на стыке ряда исследовательских программ [18-23], реализуемых в рамках наук о Земле. Комплексный характер подобных программ и наличие сложных прямых и обратных связей между гидрометеорологическими процессами, загрязнением природных сред, биосферой активно стимулируют разработки теоретических основ и системной организации математических моделей. На этом более высоком уровне системная организация оперирует с «простейшими» моделями как с элементарными объектами.
Применительно к математическому моделированию процессов возникновения и развития в атмосфере аварийных выбросов загрязняющих и токсичных веществ будем исходить из моделей физических процессов. К ним относятся модели гидротермодинамики атмосферы различных пространственно-временных масштабов, а также модели переноса и трансформации примесей, различные способы параметризации и т.п. В литературных источниках имеется достаточно много подобных разработок [21-23]. Их физический смысл и различия между ними зависят от конкретной постановки задач. В любом случае применительно к решению задачи методами численного моделирования исходят из понятий функций состояния и параметров.
Для удобства и краткости изложения воспользуемся операторной формой [19]. Обозначим векторную функцию состояния через
. К числу ее составляющих относятся поля гидрометеорологических элементов и концентраций загрязняющих примесей.
Вектор параметров обозначим
. Параметрами являются коэффициенты уравнений, параметры области интегрирования D
t сеточной области D
ht , области размещения наблюдательных систем D
mt , начальные значения функций состояния, распределения и мощности источников тепла, влаги и других примесей и компонентов.
В операторном виде математическая модель описываемого процесса имеет следующий вид:
Здесь:
– нелинейный дифференциальный оператор матричной структуры, действующий на множествах функций
и
;
Q(Dt) – пространство функций состояния, удовлетворяющих граничным условиям;
R(Dt) – область допустимых значений параметров;
В – диагональная матрица, в которой все или часть элементов могут быть нулями;
– источники;
– , где D – область изменения пространственных переменных;
– интервал изменения времени t.
Входящий в соотношение (1.1) оператор
– определяется уравнениями гидротермодинамики системы атмосфера – почва – вода, переноса и трансформации примесей, а также условиями на границах раздела.
Граничные и начальные условия записываются для конкретного физического содержания модели.
В частности, для математической модели переноса примесей в атмосфере, которая входит в состав уравнения (1.1) в качестве составной части, получаем уравнение