Было ясно, что требовалась более сложная форма, и после успеха Грина и Шварца с нарушением четности задача нахождения этой формы вышла на первый план. Как только физикам стал бы известен точный вид многообразия, в которое сворачиваются дополнительные шесть измерений, они, наконец, смогли бы перейти от слов к делу.

Следующий шаг был предпринят в 1984 году, когда Грин, Шварц и Питер Вест из Кингс‑Колледжа заинтересовались K3‑поверхностями – широким классом комплексных многообразий, который изучался математиками уже более столетия, хотя внимание именно физиков K3 привлекли, когда мои доказательства гипотезы Калаби показали, что эти поверхности могут поддерживать риччи‑плоскую метрику. «Я понял, что компактное пространство должно быть риччи‑плоским, для того чтобы космологическая постоянная пространства более низкой размерности, в котором мы живем, не была положительной – как и требовали все теории того времени», – вспоминает Шварц.[55] В свете последующего открытия темной энергии, предполагающей наличие чрезвычайно малой, но все же положительной космологической постоянной, пришлось разработать более сложные варианты теории, предполагающей возникновение очень малой космологической постоянной в нашем четырехмерном мире из компактных риччи‑плоских пространств, – об этом пойдет речь в десятой главе.

Поверхность K3, обязанная своим названием горе K2 и трем математикам, исследовавшим геометрию подобных пространств, – Эрнсту Куммеру, упоминавшемуся ранее Эриху Кэлеру и Кунихико Кодайра, – была выбрана для предварительной проверки несмотря на наличие у нее только четырех вещественных (или двух комплексных) измерений вместо требуемых шести, во многом благодаря тому, что коллеги убедили Грина, Шварца и Веста в отсутствии аналогов этих многообразий более высокой размерности. Однако, как говорит Грин: «Я совершенно уверен в том, что мы нашли бы способ расставить все по местам… даже если бы в то время и не получили этой информации [о существовании шестимерных аналогов риччи‑плоских K3 поверхностей]».[56] «То, что исследование было начато с испытанных K3 поверхностей, – добавляет Шварц, – было обусловлено совсем не желанием найти подлинный вид компактификации. Мы просто хотели поиграть, посмотреть, что мы получим в результате и как это связано с сокращением аномалий».[57] С тех пор поверхности K3 имеют неоценимое значение для струнных теоретиков, исполняя роль «игрушечных моделей» для компактификации. Они также незаменимы при исследовании двойственностей в теории струн, о которых пойдет речь в следующей главе.

Примерно в то же время, в 1984 году, физик Эндрю Строминджер, сейчас работающий в Гарварде, а тогда – в Институте перспективных исследований (ИПИ) в Принстоне, объединил свои усилия с физиком‑теоретиком Филиппом Канделасом, сейчас работающим в Оксфорде, а тогда – в Техасском университете, для того чтобы определить класс шестимерных пространств, удовлетворяющий строгим условиям теории струн. Им было известно, что внутренние пространства этих шестимерных многообразий должны быть компактными, чтобы иметь возможность перейти от десяти к четырем измерениям, а кривизна должна удовлетворять как уравнениям теории гравитации Эйнштейна, так и требованиям симметрии, налагаемым теорией струн. Эти исследования в конце концов привели их и еще двоих их коллег – Гари Горовица из Калифорнийского университета и Виттена – к тем пространствам, существование которых я установил, доказав гипотезу Калаби, хотя Виттен пришел к этим многообразиям собственным путем. «Одной из важнейших особенностей открытий в современной науке является то, что физики и математики по совершенно разным причинам зачастую приходят к одним и тем же структурам, – делится своим наблюдением Строминджер. – Порой физики обгоняют математиков, порой математики обгоняют физиков. В данном случае математики оказались впереди. Им удалось понять важность этих пространств раньше нас».[58]

То, что говорит Строминджер, несомненно является правдой, но так же верно и то, что математики, и в их числе я сам, изначально не имели ни малейшего представления о связи пространств Калаби‑Яу с физикой. Причина, по которой я занялся исследованием этих пространств, состояла в том, что я находил их чрезвычайно красивыми; именно их необычайная красота зародила во мне подозрение, что физики обязательно должны взглянуть на них повнимательнее, что эти пространства содержат в себе множество загадок, достойных того, чтобы быть открытыми. В конечном итоге, именно физикам предстояло создать эту связь, построив мост между геометрией и физикой и положив тем самым начало долгому и продуктивному сотрудничеству между двумя областями знаний – сотрудничеству, которое процветает и по сей день.

История установления этой связи интересна сама по себе. Строминджер подытожил ее следующим образом: «Суперсимметрия позволила перебросить мост к голономии, а голономия стала мостом к пространствам Калаби‑Яу».[59]

Как вы помните, мы кратко обсудили суперсимметрию в четвертой главе, в контексте вопроса об одной из разновидностей внутренней – ограниченной симметрии – в отличие от более радикальной, глобальной, симметрии такого объекта, как, например, сфера, – которую должны были демонстрировать многообразия Калаби‑Яу будучи классом кэлеровых многообразий. Эта внутренняя симметрия представляет собой часть того, что мы подразумеваем под термином «суперсимметрия», но прежде чем мы попытаемся нарисовать ясную картину, скажем несколько слов о голономии.

Грубо говоря, голономия является мерой, характеризующей поведение касательных векторов для определенной поверхности при попытке их параллельного переноса по петле, охватывающей данную поверхность. Представьте, к примеру, что вы стоите на Северном полюсе и держите в руке копье, направленное по касательной к земной поверхности. Сначала вы движетесь строго в направлении экватора вдоль того направления, в котором указывает ваше копье. Достигнув экватора, вы обнаружите, что теперь ваше копье направлено перпендикулярно экватору в сторону Южного полюса. После этого, двигаясь по экватору, вы обходите половину земной окружности, держа копье направленным на юг. Пройдя это расстояние, вы вновь держите путь на Северный полюс, не меняя направления копья. Оказавшись на Северном полюсе, вы неожиданно обнаружите, что, несмотря на все ваши старания, копье, которое вы держали в руках, оказалось повернутым на 180 градусов относительно первоначального направления.

Мы могли бы повторить этот процесс любое число раз, совершая более длинные или более короткие путешествия вдоль экватора, каждый раз обнаруживая, что копье повернулось на некоторый угол, иногда меньше 180 градусов, иногда больше – в зависимости от длины нашего пути по экватору. Для того чтобы определить голономию нашей планеты, которую в первом приближении можно считать двухмерной сферой, рассмотрим все возможные пути – или все возможные петли, – которые можно проложить на ее поверхности. Оказывается, на поверхности сферы можно получить любой наперед заданный угол поворота от 0 до 360 градусов, делая соответствующую петлю больше или меньше. Можно даже получить угол больше 360 градусов, пройдя один и тот же путь два или более раз. Принято говорить, что двумерная сфера относится к группе голономии SO(2) или к специальной ортогональной группе 2, содержащей в себе все возможные углы. Сферы более высоких размерностей относятся к группам SО(n ), содержащим все возможные вращения, сохраняющие ориентацию, а n относится к числу измерений.

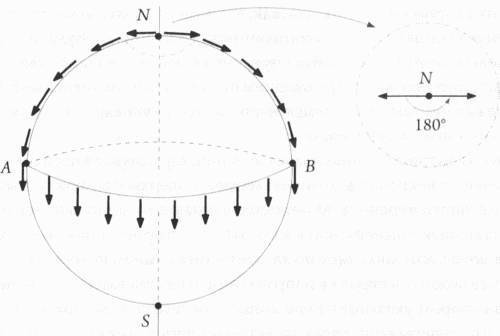
Рис. 6.1. Одним из способов классификации пространства или поверхности является его классификация при помощи голономии , показывающей, что происходит с касательным вектором при параллельном переносе в таком пространстве – то есть перемещении, при котором мы стремимся сохранить направление вектора, несмотря на искривленность траектории. В данном примере, взяв на северном полюсе касательный вектор, направленный в точку А, мы начинаем движение в сторону экватора. По достижении экватора оказывается, что вектор теперь направлен на юг. Сохраняя это направление, мы перемещаемся вдоль экватора из точки А в точку В, проходя при этом половину земной окружности. После этого мы опять движемся на северный полюс, вновь сохраняя направление вектора неизменным. Оказавшись на северном полюсе, мы неожиданно обнаруживаем, что вектор оказался повернутым на 180 градусов относительно первоначального направления, несмотря на все наши попытки сохранить его направление неизменным