Зигель был вовсе не первым, предпринявшим такую попытку. В 1895 году Генрих Вебер закончил работу над вторым изданием «Собрания трудов» Римана, после чего отдал его бумаги на хранение в университетскую библиотеку. Когда там появился Зигель, бумаги пролежали среди архивов в Геттингене (где они находятся и по сей день, см. главу 22.i) уже 30 лет. Разные исследователи неоднократно предпринимали попытки изучить эти записи, но все в конце концов отступали перед фрагментарным и неорганизованным стилем черновиков Римана, или же, вполне вероятно, им просто не хватало математической квалификации для понимания этих записей.
Зигель был сделан из более крутого теста. Он не отступил и продолжал изучать толстые кипы небрежно исписанных листков и в результате сделал потрясающее открытие, которое и опубликовал в 1932 году в статье под названием «О Nachlass[146] Римана, относящихся к аналитической теории чисел». Это одна из ключевых работ в истории Гипотезы Римана. Чтобы объяснить суть сделанного Зигелем открытия, нам надо вернуться к вычислительной линии повествования — другими словами, к попыткам реально вычислить нули дзета-функции и проверить Гипотезу Римана экспериментально.
IV.
В нашем рассказе о вычислительном направлении в главе 12 мы остановились на Йоргене Граме, который в 1903 году опубликовал результаты вычисления 15 первых нетривиальных нулей. Работа в этом направлении не прекращается по сей день. В 1996 году на конференции по Гипотезе Римана в Сиэтле Эндрю Одлыжко представил историю вопроса, которая показана в таблице 16.1.
| Исследователь(и) | Дата опубликования | Число нулей с вещественной частью 1/2 |
| Й. Грам | 1903 | 15 |
| Р.Дж. Бэклунд | 1914 | 79 |
| Дж. И. Хатчинсон | 1925 | 138 |
| Э.Ч. Титчмарш и др. | 1935-1936 | 1041 |
| А.М. Тьюринг | 1953 | 1054 |
| Д.Х. Лемер | 1956 | 25 000 |
| Н.А. Меллер | 1958 | 35 337 |
| Р.Ш. Леман | 1966 | 250 000 |
| Дж. Б. Россер и др. | 1969 | 3 500 000 |
| Р.П. Бренти др. | 1979 | 81 000 001 |
| X. те Риле, Я. ван де Луне и др. | 1986 | 1 500 000 001 |
Таблица 16.1. Вычисление нулей дзета-функции.
В конце 2000 года ван де Луне довел вычисления до 5 миллиардов нулей дзета-функции Римана, а в октябре 2001 года — до 10 миллиардов. Тем временем в августе 2001 года Себастьян Веденивски, использовав свободные процессорные мощности на 550 офисных персональных компьютерах корпорации IBM в Германии, инициировал проект по дальнейшему развитию этих вычислений. Последний опубликованный результат Веденивски датируется 1 августа 2002 года; число нетривиальных нулей с вещественной частью одна вторая доведено до 100 миллиардов.
Здесь на самом деле происходит несколько вещей сразу, и важно четко их разделять.
Во-первых, не следует смешивать а) высоту вдоль критической прямой и б) число нулей. «Высота» означает просто мнимую часть комплексного числа: высота числа 3 + 7i равна 7. При рассмотрении нулей дзета-функции принято обозначать высоту буквой t или T. (Поскольку мы знаем, что нули симметричны относительно вещественной оси, мы интересуемся только положительными t). Имеется формула для числа нулей вплоть до высоты T:
N(T) = T/2π∙ln (T/2π) − T/2π + Ο(ln T)
Это на самом деле очень хорошая формула (первые два слагаемых в ней принадлежат Риману): она дает превосходное приближение уже для достаточно малых значений T. Если не обращать внимания на член с Ο большим[147], то для T, равного 100, 1000 и 10 000 она дает соответственно 28,127, 647,741 и 10 142,090. Истинное же число нулей на этих высотах составляет 29, 649 и 10 142. Чтобы получить значение N(T) величиной в 100 миллиардов, как у Веденивски, требуется взять T равным 29 538 618 432,236… — до такой высоты Веденивски и добрался в своих исследованиях.
Далее, имеется путаница по поводу того, что именно вычисляется. Не предполагается, что Веденивски способен предъявить все 100 миллиардов этих нулей, вычисленных с высокой (или даже со средней) точностью. Цель подобных исследований состоит главным образом в подтверждении Гипотезы Римана, а это можно сделать, не прибегая к высокоточным вычислениям нулей. Имеются некоторые теоретические построения, позволяющие вычислить, сколько нулей имеется в критической полосе между высотами T1 и T2 — т.е. внутри прямоугольника, верхняя и нижняя стороны которого задаются числами T1 и T2, отложенными вдоль мнимой оси, а левая и правая сторона — числами 0 и 1 на вещественной оси, как показано на рисунке 16.1. Имеется и другое теоретическое построение, которое позволяет вычислить, сколько нулей расположено на критической прямой между данными высотами.[148] Если два вычисления дают один и тот же результат, то можно считать, что вы тем самым подтвердили Гипотезу Римана в данном интервале. Это можно сделать, имея лишь грубое знание о том, где на самом деле расположены нули. Большая часть таблицы 16.1 относится к работе такого сорта.
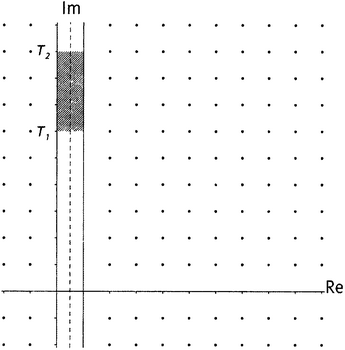
Рисунок 16.1. Высоты T1 и Т2 на критической полосе.
А как обстоит дело с табулированием точных положений нулей? Оказывается, помимо того, что делалось в связи с проверкой Гипотезы Римана, в этой задаче сделано на удивление мало. Насколько мне вообще известно, первые сколько-нибудь длинные таблицы такого рода были опубликованы Брайаном Хейзелгровом. В 1960 году, работая на мощных компьютерах второго поколения в университетах Кембриджа и Манчестера в Англии, Хейзелгров с сотрудниками затабулировали первые 1600 нулей с точностью до шести знаков после запятой и опубликовали эту таблицу. Эндрю Одлыжко сообщил мне, что, когда он в конце 1970-х годов начинал исследования нулей дзета-функции, таблицы Хейзелгрова были единственными известными ему данными такого рода, хотя он и думает, что Леман в ходе своей работы в 1966 году мог в действительности с высокой точностью вычислить большее количество нулей. У самого Эндрю есть таблица (на диске компьютера, а не в печатном варианте) первых двух миллионов нулей с точностью до девяти знаков после запятой. На момент написания этой книги это наибольшая из известных таблиц нулей.
Вся описанная выше деятельность относится к первым N нулям. Кроме этого, Эндрю Одлыжко совершил несколько «прыжков» вверх с целью исследовать небольшие изолированные отрезки на очень больших высотах. Он опубликовал результат вычисления самого высокорасположенного нетривиального нуля дзета-функции из известных на данный момент — это 10 000 000 000 000 000 010 000-й нуль. С точностью до пяти знаков после запятой в мнимой части он расположен в точке 1/2 + 1 370 919 909 931 995 309 568,33539i. Эндрю вычислил и первые 100 нулей с точностью до тысячи знаков после запятой.[149] Первый нуль начинается как (имеется в виду, конечно, мнимая часть):