Альтернативным способом функцию можно представить, показав картинку типа «сюда» на плоскости значений.[115] Вместо того чтобы показывать, как это делалось на рисунках 13.6 и 13.7, какие аргументы отправляются в интересные нам значения (а такими у нас были чисто вещественные и чисто мнимые числа), можно дать картину плоскости значений, на которой будет показано, в какие значения отображаются интересующие нас аргументы.
Представим себе, что у муравья Арга есть брат-близнец, который живет на плоскости значений.{A4} Зовут его, понятно, муравей Знач. И допустим еще, что близнецы постоянно общаются между собой по рации и таким способом синхронизируют свои передвижения, так что, на каком бы аргументе ни находился муравей Арг в любой момент времени, муравей Знач стоит на соответствующем значении в плоскости значений. Если, например, муравей Арг стоит на числе 1/2 + 14,134725i, а на его приборчике выставлена дзета-функция, то муравей Знач стоит на числе 0 в своей плоскости (плоскости значений).
Предположим теперь, что муравей Арг, вместо того чтобы ползать по всем этим причудливым завитушкам, изображенным на рисунке 13.6 (что заставляет муравья Знача скучать, вышагивая взад и вперед по вещественной и мнимой осям), предпримет прогулку прямо по критической прямой, направляясь на север из аргумента 1/2. По какой траектории будет тогда следовать муравей Знач? Это показано на рисунке 13.8. Его путь начинается в точке ζ(1/2), что, как мы видели в главе 9.v, равно −1,4603545088095…. Далее он описывает нечто вроде полуокружности против часовой стрелки ниже нулевой точки, а затем поворачивает и движется по петле по часовой стрелке вокруг точки 1. Он держит путь к нулю и проходит через него (это первый нуль — муравей Арг как раз прошел точку 1/2 + 14,134725i). Затем он продолжает описывать петли по часовой стрелке, проходя через нулевую точку снова и снова через некоторый промежуток — всякий раз, как его брат-близнец наступает на нуль дзета-функции на плоскости аргумента. Я прервал путешествие Знача, когда муравей Арг достиг точки 1/2 + 35i, потому что рисунок 13.6 продолжается лишь до этих пор. К тому моменту, как эта точка достигнута, кривая на плоскости значений прошла через нуль пять раз, что соответствует пяти нетривиальным нулям на рисунке 13.6. Отметим, что точки на критической прямой демонстрируют выраженную тенденцию к тому, чтобы отображаться в точки с положительной вещественной частью.
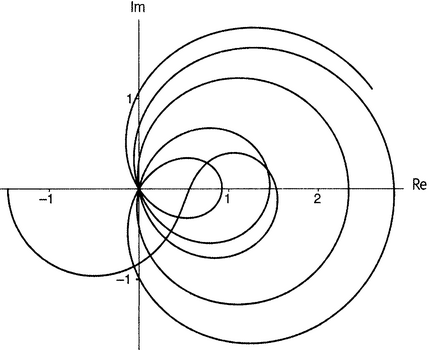
Рисунок 13.8. Плоскость значений; показаны точки, которые приходят из критической прямой.
Еще раз: на рисунке 13.8 показана плоскость значении. Это не диаграмма типа «отсюда», подобная рисункам 13.6 и 13.7; наоборот, это диаграмма типа «сюда», которая показывает, что же дзета-функция делает с критической прямой, подобно тому как на рисунке 13.2 было показано, что функция возведения в квадрат делаете расчерченным квадратиком. Если мы желаем выражаться чисто математически, то следует сказать, что завивающаяся в петли кривая на рисунке 13.8 есть ζ(критическая прямая) — множество всех точек, которые происходят из точек на критической прямой. Кривые на рисунках 13.6 и 13.7 суть ζ−1(вещественная и мнимая оси) — множество всех точек, которые дзета-функция отправляет в вещественную и мнимую оси. Мы используем запись «ζ(критическая прямая)», чтобы указать на «все значения дзета-функции при аргументах, лежащих на критической прямой». Наоборот, «ζ−1(вещественная и мнимая оси)» означает «все аргументы, для которых значения дзета-функции лежат на вещественной или мнимой осях». Заметим, что выражение ζ−1 используется здесь в специальном смысле теории функций и указывает на обратную функцию. Не следует путать его с a−1 из 8-го правила действий со степенями, где имеется в виду 1/a, арифметическое обратное числа a. Это другое использование — еще один пример перегрузки математических символов, как и с буквой π, которая обозначает и число 3,14159…, и функцию числа простых чисел.
Вообще говоря, картинки типа «отсюда» на плоскости аргумента — предпочтительное средство для понимания того, что такое функция во всем охвате ее свойств (например, где расположены ее нули). Картинки «сюда» на плоскости значений полезнее всего для изучения конкретных аспектов или любопытных особенностей функции.[116]
Гипотеза Римана утверждает, что все нетривиальные нули дзета-функции лежат на критической прямой — прямой, составленной из комплексных чисел с вещественной частью одна вторая. Все нетривиальные нули, изображенные в этой главе, действительно лежат на этой прямой, что видно из рисунка 13.6, 13.7 и 13.8. Конечно, это ничего не доказывает. У дзета-функции бесконечное число нетривиальных нулей, и никакой рисунок не позволит изобразить их все. Откуда нам знать, что триллионный нуль, или триллион триллионный, или же триллион триллион триллион триллион триллион триллионный лежит на критической прямой? Этого мы не знаем — во всяком случае, не можем заключить из картинок. А какое отношение все это имеет к простым числам? Чтобы ответить на этот вопрос, нам надо повернуть Золотой Ключ.
Глава 14. Во власти одержимости
I.
Геттинген, конечно, был не единственным местом на земле, где в первые годы XX века создавалась первоклассная математика. Взглянем на английского математика Джона Идензора Литлвуда за шестьдесят с чем-то лет до того, как он предлагал «понюхать пороху» Хью Монтгомери. В 1907 году, будучи молодым математиком в Тринити-колледже в Кембридже, Литлвуд был занят поиском содержательной задачи, из которой удалось бы вырвать хороший «кусок мяса» для диссертации.
Барнс[117] решился предложить такую новую задачу: «Доказать Гипотезу Римана». В конце концов оказалось, что это героическое предложение привело к некоторым результатам; но сначала надо сказать о ситуации с ζ(s) и с простыми числами на 1907 год, в особенности в том плане, как я ее воспринимал. Я впервые познакомился с ζ(s) у Линделёфа[118], но там вообще ничего не говорится о простых числах, а я и не догадывался о существовании какой бы то ни было связи между ними. Я знал, что ГР — знаменитая гипотеза, но полагал, что это просто проблема из теории целых функций. А все это происходило в течение долгих каникул, когда у меня не было доступа к литературе (даже если бы мне пришло в голову заняться какими-нибудь поисками). (Что касается людей образованных лучше меня, то лишь некоторые слышали о работе Адамара и лишь совсем немногие — о статье де ля Валле Пуссена в каком-то бельгийском журнале. Во всяком случае, та деятельность воспринималась как очень сложная и проходящая в стороне от основного течения математики. Знаменитая статья Римана была включена в собрание его трудов; в ней утверждается ГР и потрясающая, но не доказанная формула для π(x). Сама Теорема о распределении простых чисел не упоминается, хотя ее ничего не стоит получить, если принять приведенную там формулу. Что же касается Харди, то, как он впоследствии сказал мне, он знал, что ТРПЧ была доказана, но, правда, думал, что это сделал Риман. Все изменилось в мгновение ока с выходом в свет книги Ландау в 1909 году.)