Слава создателей неевклидовой геометрии по праву принадлежит двум другим математикам: Лобачевскому и Бойаи. В действительности их труды явились своего рода эпилогом в развитии идей, высказанных ранее другими учеными, но поскольку они опубликовали первые систематические изложения неевклидовой геометрии, именно они и признаны ее создателями. Русский математик Николай Иванович Лобачевский (1793-1856) закончил Казанский университет, профессором и ректором которого стал впоследствии (1827-1846). Начиная с 1825 г. он представил свои соображения по основаниям геометрии в многочисленных статьях и двух книгах. Янош Бойаи (1802-1860), сын известного венгерского математика Фаркаша Бойаи, был офицером австро-венгерской армии. Свою работу (объемом в 26 страниц) по неевклидовой геометрии под названием «Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида, что a prioriникогда решено быть не может, с прибавлением к случаю ложности геометрической квадратуры круга» Бойаи опубликовал в качестве приложения к первому тому сочинения своего отца «Опыт введения учащегося юношества в начала чистой математики» (Tentamen juventutem studiosam in elementa Matheoseos).Хотя эта книга вышла в 1832-1833 гг., т.е. после первых публикаций Лобачевского, Бойаи, по-видимому, разработал свои идеи по неевклидовой геометрии еще в 1825 г. и убедился в ее непротиворечивости.
Гаусс, Лобачевский и Бойаи поняли, что аксиома Евклида о параллельных не может быть доказана на основе девяти остальных аксиом евклидовой геометрии и что для обоснования последней необходима какая-то дополнительная аксиома. Так как аксиома о параллельных независима от остальных аксиом, представляется возможным (по крайней мере чисто логически) заменить ее противоположной аксиомой и попытаться вывести следствия из новой системы аксиом.
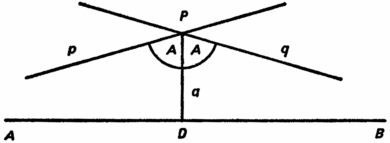
С чисто математической точки зрения содержание работ Гаусса, Лобачевского и Бойаи очень просто. Суть дела удобнее всего пояснить на примере геометрии Лобачевского, ибо все трое по существу сделали одно и то же. Отвергнув аксиому Евклида о параллельных, Лобачевский фактически принял такое же допущение, каким некогда воспользовался Саккери. Если дана прямая ABи точка Pвне ее (рис. 34), то все прямые, проходящие через точку P, распадаются относительно прямой ABна два класса, а именно на класс прямых, пересекающихся с прямой ABи класс прямых, не пересекающихся с прямой AB. Точнее если точка Pлежит на перпендикуляре к прямой ABна расстоянии aот нее, то существует острый угол A , такой, что все прямые, образующие с перпендикуляром PDугол меньше A,пересекаются с прямой AB, а прямые, образующие с PDугол больше A,не пересекаются с прямой AB.Две прямые pи q, образующие с перпендикуляром PDугол A , называются параллельными, а сам угол A называется углом параллельности. Прямые, проходящие через точку Pи не пересекающиеся с прямой AB, но отличные от параллельных pи q, называются расходящимися с прямой ABили сверхпараллельными ей (с точки зрения Евклида это прямые, параллельные прямой AB). В этом смысле в геометрии Лобачевского существует бесконечно много параллельных, проходящих через точку P.
Далее Лобачевский доказывает несколько ключевых теорем. Если A= π/2, то получается аксиома Евклида о параллельных. Если угол A — острый, то при a, стремящемся к нулю, Aвозрастает до π/2, а при неограниченном возрастании aубывает до нуля. Сумма углов треугольника в геометрии Лобачевского всегда меньше 180° и стремится к 180° с уменьшением площади треугольника. Два подобных треугольника в геометрии Лобачевского непременно конгруэнтны.
Но, пожалуй, самое главное состоит в том, что неевклидова геометрия пригодна для описания свойств физического пространства ничуть не в меньшей мере, чем евклидова геометрия.Необходимость евклидовой геометрии как геометрии физического пространства ниоткуда не следует, ее физическая истинность не может быть гарантирована на основе априорных соображений. К пониманию этого немаловажного обстоятельства, не требующему никаких чисто математических доказательств, ибо все уже было сделано раньше, первым пришел Гаусс.
Но не так-то легко расстаться с накопленным ранее богатством. По-новому взглянув на природу истинного в математике, Гаусс увидел ту опору, за которую можно ухватиться. В письме Генриху В.М. Ольберсу (1758-1840) от 28 апреля 1817 г. Гаусс сообщал:
Я прихожу все более к убеждению, что необходимость нашей геометрии не может быть доказана, по крайней мере человеческимрассудком и для человеческого рассудка. Может быть, в другой жизни мы придем к другим взглядам на природу пространства, которые нам теперь недоступны. До тех пор геометрию приходится ставить не в один ранг с арифметикой, существующей чисто и a priori, а скорее с механикой.
([23], с. 103.)
Гаусс в отличие от Канта не считал законы механики априорными истинами. Он, как и многие другие, разделял взгляды Галилея, считавшего, что законы механики выводятся из опыта. Гаусс утверждал, что истина лежит в арифметике и, следовательно, в алгебре и анализе, построенных на арифметике, ибо арифметические истины интуитивно ясны нашему разуму.
Лобачевский также размышлял над применимостью своей геометрии к физическому пространству и доказал, что она применима к очень большим геометрическим фигурам. Таким образом, к 30-м годам XIX в. неевклидова геометрия не только получила признание, но и ее применимость к реальному физическому пространству была обоснована.
На протяжении примерно тридцати лет после публикации работ Лобачевского и Бойаи математики игнорировали неевклидову геометрию, видя в ней своего рода логический курьез. Некоторые из них даже не отрицали логической непротиворечивости новой геометрии. Другие были убеждены, что в неевклидовой геометрии непременно должны быть скрыты какие-то противоречия, и на этом основании считали ее бессмысленной. И почти все математики выражали уверенность, что геометрия реального пространства, настоящаягеометрия (не то что всякие выдумки), — это геометрия Евклида. Уильям Р. Гамильтон (1805-1865), несомненно, один из самых выдающихся математиков своего времени, в 1837 г. так выразил свое неприятие неевклидовой геометрии:
Ни один честный и здравомыслящий человек не может усомниться в истинности главных свойств параллельныхв том виде, как они были изложены в «Началах» Евклида две тысячи лет назад, хотя вполне мог бы желать увидеть их изложенными более просто и ясно. Геометрия Евклида — не содержит неясностей, не приводит мысли в замешательство и не оставляет разуму сколько-нибудь веских оснований для сомнения, хотя острый ум извлечет для себя пользу, пытаясь улучшить общий план доказательства.
([13], с. 113.)
Выступая в 1883 г. перед Британской ассоциацией содействия развитию наук, ее президент Артур Кэли (1821-1895) по существу поддержал точку зрения Гамильтона:
По моему мнению, двенадцатая аксиома Евклида [называемая также пятым постулатом, или аксиомой о параллельности] в форме Плейфера не требует доказательства, но является составной частью нашего представления о пространстве, физическом пространстве нашего опыта, с которым каждый знакомится на своем опыте, — представления, лежащего в основе всего нашего опыта… Утверждения геометрии не являются лишь приближенно истинными. Они остаются абсолютно истинными в отношении той евклидовой геометрии, которая так долго считалась физическим пространством нашего опыта.
([13], с. 113.)