Не мезоны и кварки, а числа и функции являлись объектом внимания ученого. Они тоже имели траектории и орбиты. Ему приходилось исследовать их поведение. Используя термин, который позже станет ходовым в новой науке, можно сказать, что Файгенбауму требовалось добиться интуитивного прозрения, которое отлилось бы в теорию и методологию. Спектрометр, ускоритель частиц и пузырьковую камеру ему заменил компьютер. Обычно пользователь формулирует задачу, программирует ее, вводит в вычислительную машину и ждет решения — одного для каждой конкретной проблемы. Файгенбаум и те, кто шел по его стопам, нуждались в большем. Требовалось повторить проделанное Лоренцем — создать миниатюрные вселенные и наблюдать за их эволюцией. Затем, меняя то или иное свойство, исследователи могли проследить, как меняются пути развития. В конечном счете они убедились, что крошечные изменения определенных качеств могут повлечь за собой значительные метаморфозы поведения системы в целом.

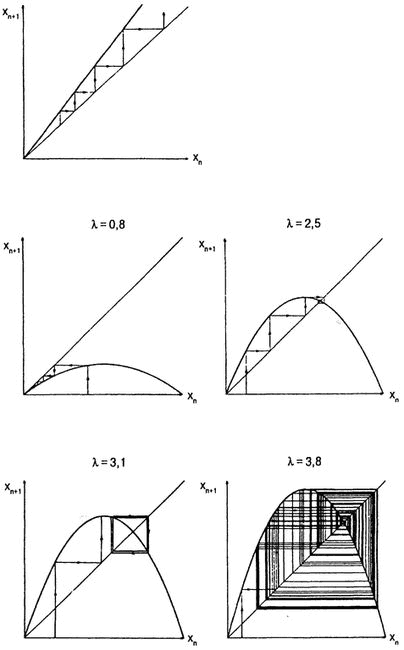
^{Рис. 6.1. Хаос под микроскопом. Простое уравнение, повторяемое много раз. Файгенбаум сосредоточился на линейных функциях, вычисляя значение одной величины в зависимости от значения другой. Для Популяций животного мира функция выражала соотношение между численностью в текущем и следующем году. Одним из способов наглядного представления таких функций является построение графика, где исходные данные отмечаются на горизонтальной оси, а конечные — на вертикальной. Для каждого значения xсуществует лишь одно значение y, и оба они образуют форму, представленную сплошной линией. Затем, чтобы изобразить долгосрочное поведение системы, Файгенбаум вычертил траекторию, начинавшуюся с произвольно взятого значения x. Поскольку каждое значение увновь подставлялось в ту же функцию в качестве новой исходной величины, ученый мог применить нечто вроде схематичного сокращения. Траектория скачками отдалялась от прямой, проведенной под углом 45°, где значения xи yравны. Для эколога наиболее очевидным типом функции, отображающей рост популяции, будет линейная — мальтузианская схема устойчивого и ничем не ограниченного увеличения с фиксированным ежегодным приростом (вверху слева).Более «реалистичные» функции представляют собой дугу, демонстрируя популяции. Здесь изображена так называемая логистическая карта для параболы, заданной функцией y= rx(1- x), где параметр rменяется от 0 до 4, определяя крутизну параболы. Но, как выяснил Файгенбаум, вид функции не имел значения. Действительно важным оказалось наличие у нее выпуклости. Поведение существенно зависело и от того, насколько парабола крута — от степени нелинейности, которую Роберт Мэй назвал «взлетами и падениями» (т. е. от способности живущей в естественных условиях популяции к увеличению и снижению числа составляющих ее особей). Слишком низкая парабола означала вымирание: любое начальное значение фактически приводило к нулю. Увеличение степени крутизны порождало устойчивое равновесие — ситуацию, понятную для эколога, который придерживается традиционных взглядов. Точка равновесия, находясь на любой траектории, являлась одномерным аттрактором. После определенной точки начинались разветвления, порождающие колеблющуюся популяцию с двумя периодами. Затем опять происходило удвоение периода, и еще, и еще раз, так что в конце концов траектория «успокаивалась» (внизу справа).Когда Файгенбаум попытался создать новую теорию, подобные изображения послужили ему отправной точкой. Он начал размышлять на языке итераций: функции функций, функции функций от функций и т. д.; схемы с двумя «горбами», потом с четырьмя…}

Файгенбаум быстро выяснил, что компьютеры Лос-Аламоса мало подходят для вычислений, которые он задумал. Несмотря на огромные ресурсы лаборатории, гораздо более обширные, нежели в большинстве университетов, лишь несколько терминалов могли воспроизводить графики и изображения, да и те находились в отделе вооружения. Файгенбаум намеревался наносить определенные числа в виде точек на своеобразную карту и вынужден был прибегнуть к наиболее простому из возможных методов: он использовал длинные рулоны распечаток, где просматривались линии, составленные из чередующихся пробелов, звездочек и знаков сложения. Официальная политика лаборатории заключалась в том, что один большой компьютер лучше нескольких менее мощных. Это было следствие курса «одна проблема — одно решение». Маломощные машины отбивали всякую охоту к исследованиям; к тому же, приобретая компьютер, каждый отдел должен был следовать обязательным указаниям сверху и давать в этом отчет. Лишь гораздо позже, благодаря финансовой помощи теоретического отдела, Файгенбаум получил в личное пользование вычислительную машину стоимостью 20 000 долларов. Теперь он мог видоизменять свои уравнения и мелькавшие на экране картины, перестраивать их, играя на компьютере, словно на музыкальном инструменте. Но это было позже, а пока единственные терминалы, за которыми удавалось всерьез работать с графикой, находились в строго охраняемых зонах, как говорили в лаборатории — за забором. Файгенбауму приходилось использовать терминал, соединенный телефонными кабелями с центральным компьютером. Имея дело с таким устройством, оценить истинную мощность машины на другом конце кабеля весьма сложно, — даже решение простейших задач занимало целые минуты. Чтобы отредактировать лишь одну строчку программы, приходилось, нажав клавишу «Возврат», ждать под непрерывный гул терминала, пока центральный компьютер не обслужит других пользователей.

Вычисляя, Файгенбаум непрерывно размышлял. Какая еще неизвестная математика могла породить наблюдаемые им множественные масштабные модели? Он понял: нечто в этих функциях должно быть повторяющимся, самовоспроизводящимся.Поведением исследуемой системы руководило поведение другой, скрытой внутри нее. Волнистый контур, открывшийся ученому в миг озарения, кое-что прояснял в том, как масштаб одной функции мог быть подогнан в соответствие с другой функцией. Файгенбаум применил теорию групп перенормировки, прибегнув к масштабированию, чтобы избавиться от бесконечности и получить количественные оценки. Весной 1976 г. его жизнь обрела безумный ритм, какого он не знал прежде. Погрузившись в некий транс, Файгенбаум с каким-то неистовством писал программы, что-то черкал карандашом на бумаге и вновь программировал. Он даже не обращался за помощью в компьютерный отдел: это было бы равносильно отказу от собственного компьютера и замене его телефоном, а перестройка метода работы казалась весьма рискованной. Митчелл не прерывался более чем на пять минут, иначе компьютер автоматически отключил бы его линию. Все же временами машина подводила ученого, повергая его в состояние, близкое к шоку. Так, без перерыва, он работал больше двух месяцев. Его рабочий день длился двадцать два часа. Когда он ложился спать, напряжение не покидало его, поднимая ровно через сто двадцать минут и заставляя думать с того же места, где он остановился. Силы его поддерживал лишь кофе. (Даже в лучшие времена Файгенбаум существовал исключительно на полусырых бифштексах, кофе и красном вине. Друзья подшучивали, что он получает витамины из сигарет.)

Конец этому положил врач, прописав ученому успокоительное в скромных дозах и усиленный отдых. Но к тому времени Файгенбаум уже создал универсальную теорию.

Универсальность стирала грань между прекрасным и полезным. Математиков, которые перешли определенную черту, мало волнует пригодность их теорий для вычислений, физики же, миновав некую точку, нуждаются в числах. Всеобщность вселяла надежду на то, что, решив легкую задачу, физики смогут ответить на гораздо более сложные вопросы, поскольку решения будут идентичными. Встроив свое открытие в рамки групп перенормировки, Файгенбаум придал теории такой облик, что физики могли признать ее в качестве почти стандартного инструмента вычислений.