Основные схемы подвески

Хотя существует бесконечное количество возможных комбинаций длин и наклонов рычагов подвески, мы можем разбить их на три основные схемы: равные по длине и параллельные рычаги, неравные по длине и параллельные рычаги и неравные по длине, непараллельные рычаги. Мы кратко рассмотрим характеристики каждой из них.

Равные по длине и параллельные рычаги

Самое простое – это система параллельных и коротких рычагов одинаковой длины. Поскольку рычаги образуют параллелограмм, при вертикальном перемещении развал меняться не будет. Однако наблюдается значительное изменение ширины колеи, что не очень-то хорошо. Когда шасси кренится, колесо изменяет угол развала точно на величину крена шасси – при этом внешнее колесо получает положительный развал. Это нехорошо ни при каких условиях, и чем шире используемая шина, тем хуже! Поскольку рычаги остаются параллельными при любых условиях, местоположение мгновенного центра – пересечение продолжения осей рычагов – устремляется в бесконечность от осевой линии шасси. Мы предполагаем, что центр крена находится на уровне земли и в значительной степени там и остается.

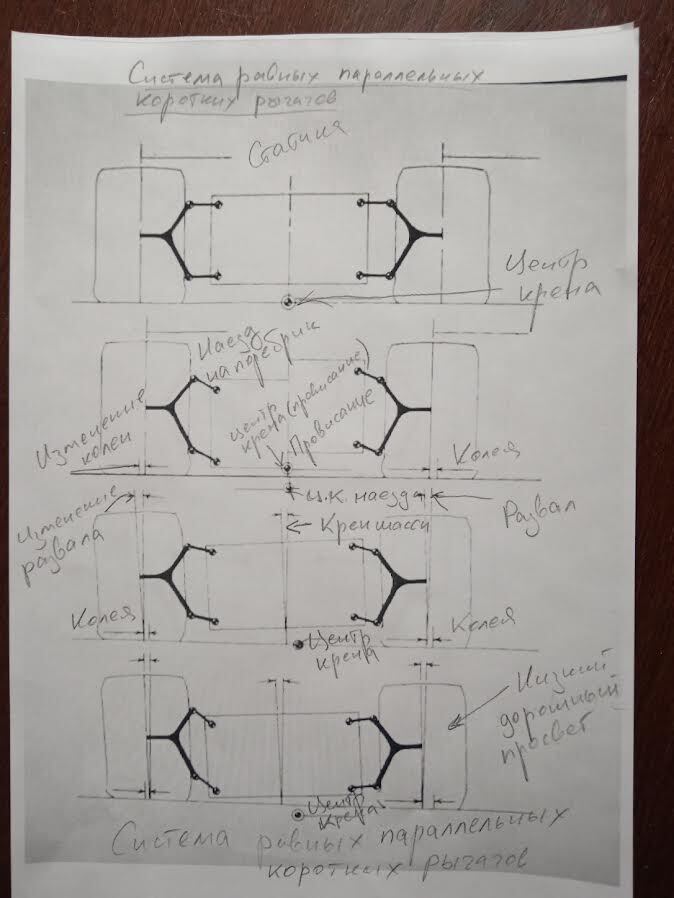
Мы можем уменьшить величину изменения колеи при заданном количестве вертикальных перемещений простым способом – удлинив рычаги подвески. При таком изменении заданная величина вертикального перемещения колеса или шасси приводит к меньшему угловому смещению колеса и, следовательно, к меньшему изменению размера колеи. Увы, геометрия рычагов остается параллелограммной, а ситуация с развалом по крену, в основном, прежняя, хотя величина изменения развала немного уменьшена, поскольку внутренние точки осей поворота расположены ближе к осевой линии автомобиля и, следовательно, смещаются меньше при заданном значении крена. Кроме того, хотя мы можем сколько-то уменьшить изменение колеи за счет удлинения рычагов, мы не сможем не только устранить его, но даже уменьшить до приемлемых пределов – и, естественно, у нас нет места для бесконечно длинных рычагов!

Неравные и параллельные рычаги

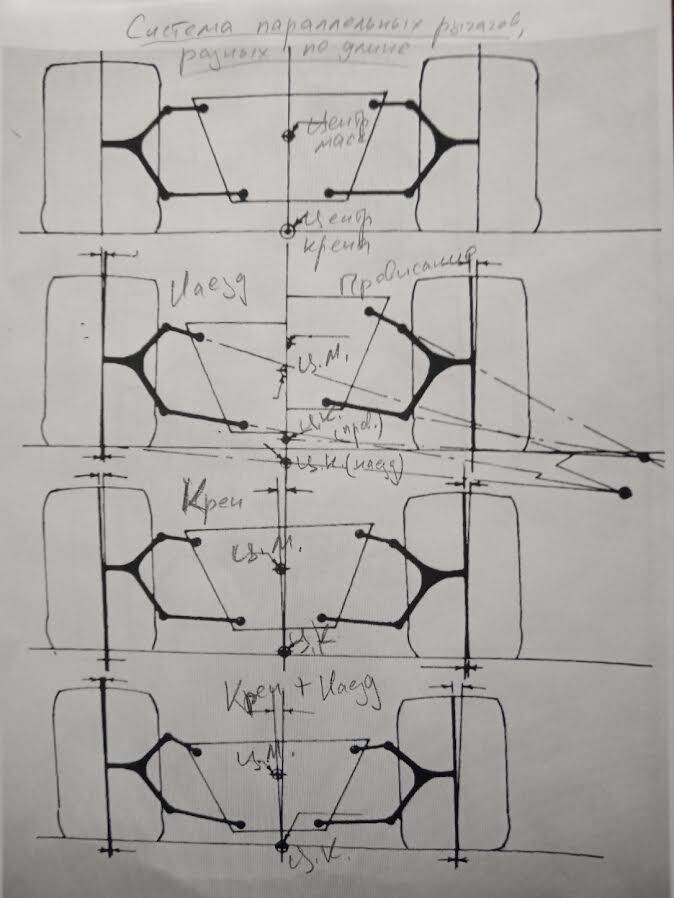
Если мы сделаем верхний рычаг относительно короче нижнего, мы добьемся некоторых существенных изменений в траектории движения колес. Теперь, при вертикальном перемещении, верхний рычаг имеет меньший радиус, чем нижний; это приводит к тому, что колесо принимает отрицательный угол развала как при наезде (например, на поребрик), так и отрицательный либо положительный развал при провисании. Величина изменения развала зависит от относительной длины верхнего и нижнего рычагов – чем короче верхний рычаг, тем круче кривая изменения развала. Допущение отрицательного развала значительно уменьшает изменение размера колеи, и при должной аккуратности в настройке оно может стать незначительным. При крене подрессоренной массы колеса по-прежнему «разваливаются» в том же направлении; однако положительный развал, который принимает на себя нагруженное колесо, значительно уменьшается. К сожалению, отрицательный развал разгруженного (внутреннего) колеса увеличивается. Все ровно так же, как на спортпрототипе Legends 600.

Несмотря на то что рычаги параллельны друг другу на уровне дорожного просвета, тот факт, что они неодинаковы по длине, означает, что они не будут оставаться параллельными при вертикальном движении колеса (они почти остаются параллельными при крене), поэтому длина повернутого рычага в моменте варьируется. Это означает, что при большой вертикальной амплитуде колеса, углы развала станут действительно очень большими. Если требуется большой вертикальный ход колеса – как в гонках по бездорожью –необходимо сделать рычаги максимально равными по длине. В любом случае, центр крена с неравными, но параллельными рычагами остается довольно стабильным по отношению к центру масс. Следовательно, момент крена остается более или менее постоянным, что хорошо. Естественно, нет закона, который гласил бы, что параллельные рычаги разной длины должны быть параллельны земле на уровне дорожного просвета, но небольшой эксперимент с любой моделью объяснит, почему они обычно параллельны земле на этом уровне. Где-то здесь Смит упоминает, что статический дорожный просвет вполне может отличаться от динамического, если для создания прижимной силы в значительных количествах используются крылья или эффективные спойлеры. Далее: динамический дорожный просвет будет меняться в зависимости от скорости движения. Еще одно небольшое усложнение, которое сегодня нам, на самом деле, не очень-то нужно.

Неравные и непараллельные рычаги

В то время как система подвески с неравными и параллельными рычагами уменьшает положительный развал нагруженного колеса при крене, она, однако, не уменьшает его в достаточной степени для определенного типоразмера шин – и, кроме того, эта система ведет к действительно низкому центру крена. Наклоняя рычаги (и продолжая, «лонгируя») их оси относительно друг друга, мы можем расположить центры крена там, где нам заблагорассудится, – по крайней мере, в статическом положении, – и еще больше уменьшить положительный развал нагруженного колеса при крене. Естественно, абсолютизируя процесс можно дойти до экстремальных результатов, однако именно так понятно, что может произойти, когда мы заходим слишком далеко в любом заданном направлении настроек.

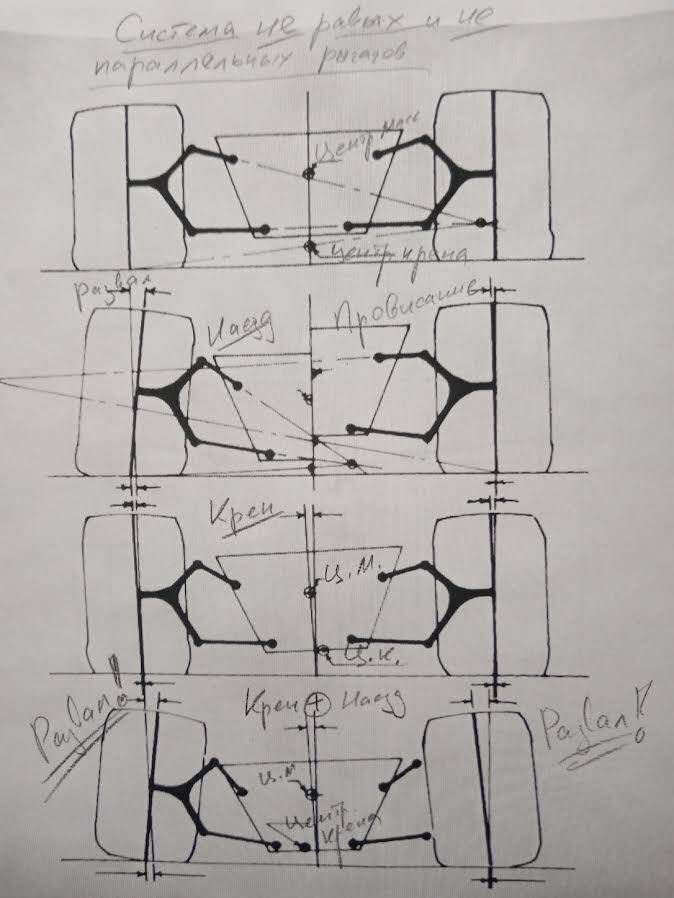
Возьмите листок бумаги, ручку и линейку – и попробуйте поэкспериментировать. В предельном случае наклон верхнего рычага вниз по направлению к центральной линии болида действительно заметно уменьшает положительный развал нагруженного колеса при крене шасси. Но это также повлияло на все остальное! Произошло то, что слишком крутой наклон верхнего рычага приводит к очень короткому плечу в моменте с сопутствующим очень большим углом развала при перемещении колеса со стороны дороги (пусть это будет, к примеру, наезд на высокий поребрик). Подняв кузовные точки крепления как верхнего, так и нижнего рычагов, мы добились бы гораздо лучших углов развала при сохранении статичного центра крена в том же положении – однако, конечно, тогда в динамике центр крена перемещался бы больше. Как мы уже подметили, игра в «идеальную геометрию» может продолжаться вечно…

Важные истины и компромиссный баланс

После того как мы вдоволь прошлись по всем основным схемам, некоторые важные истины становятся очевидны:

1. Хотя можно контролировать развал колеса как при вертикальном перемещении, так и при крене шасси, добиться очень хорошего контроля развала в комбинированных («бампинг» + крен) условиях невозможно, – мы всегда в положении "или-или".

2. Чем длиннее мы делаем рычаги подвески, тем меньшее угловое и линейное смещение колес произойдет в результате заданного количества перемещений шасси или колес.

3. При вертикальном перемещении центр крена трансформируется вместе с центром масс, стремясь сохранить постоянный момент крена.

4. Увеличение эффективной длины рычага уменьшает величину изменения развала из-за вертикального перемещения колеса, уменьшает величину вертикального перемещения центра крена относительно центра масс и увеличивает боковое перемещение центра крена.