Однако перед тем как мы будем разбираться в новой коллапсирующей функции основанной на Махло кардинале, следует вспомнить, что из-за недоказуемости обобщенной континуум-гипотезы мы были вынуждены разделить недостижимые кардиналы на слабонедостижимые и сильнонедостижимые, так же как раньше разделили несчетные на алеф-кардиналы и бет-кардиналы, это же придется сделать и с Махло кардиналом. Махло кардинал для которого стационарно множество регулярных алеф-кардиналов (и соответственно слабонедостижимых тоже) будет называться Слабым Махло кардиналом, а Махло кардинал для которого стационарно множество регулярных бет-кардиналов (и соответственно сильнонедостижимых тоже) будет называться Сильным Махло кардиналом. Если предположить правильность континуум-гипотезы, то Слабый Махло кардинал и Сильный Махло кардинал это один и то же кардинал, однако если предположить ложность континуум-гипотезы, то так же как это было с недостижимыми: Слабый Махло кардинал < Сильный Махло кардинал, и мы так же не можем предположить насколько первый меньше второго, он может быть даже меньше континуума (ב1).
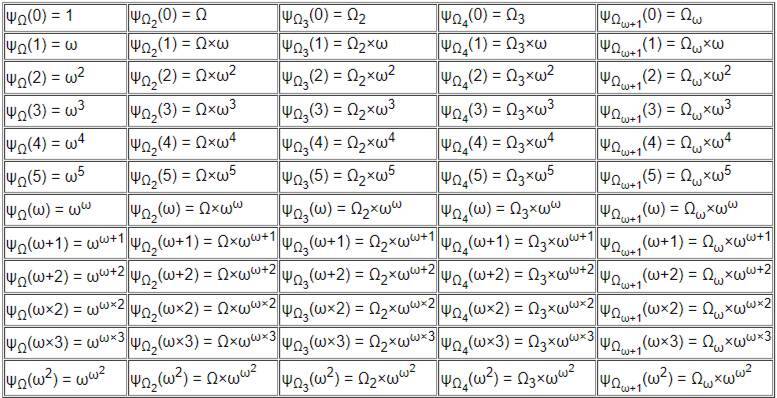
Функция Бухольца принимала в себя два аргумента: ψπ(n) – где π – это регулярный кардинал, на основе которого происходит коллапсирование, а n – это ординал, основной аргумент функции, который собственно и коллапсируется, он может быть любым, но не должен превосходить по кардинальности π. В целом функция ψπ(n), в случае |n| = π, на выходе понижала кардинальность n, но увеличивала рекурсию получившегося ординала, так что ψΩk+1(Ωk+1) = εΩk+1, и ψΩk(Ωk+α) = ωψΩk(Ωk)+α.
Здесь придём к функции Ратъена. На самом деле это не одна, а целых две функции, и кроме ψ-функции Ратъен определил еще и χ-функцию. Принципиальное отличие между ними заключается в том, что если ψ-функция возвращает любые ординалы, то χ-функция возвращает всегда только регулярные ординалы. По определению, если n < I, то χ(n) – возвращает n-ный несчетный регулярный ординал (считая с нуля). Тут важно отметить, что ω-ный регулярный ординал это ωω+1, потому что, как вы должны помнить из прошлой части, |ωω| = ℵω – регулярным не является. Следовательно, пользуясь обозначениями коллапсирующей функции, мы получим следующие преобразования: χ(0) = Ω, χ(1) = Ω2, χ(2) = Ω3, χ(ω) = Ωω+1, χ(Ω) = χ(χ(0)) = ΩΩ+1, χ(Ω) = χ(χ(1)) = ΩΩ+2, χ(ΩΩΩΩ…) = Ω(ΩΩΩ…+1) = ΩФ(1,0)+1, и т.д. В целом, принципы коллапсирования позволяют определить общее свойство χ(n) = Ωn+1, гласящее что n-ный несчётный кардинал равен кардиналу, который предшествует n-ному несчетному регулярному кардиналу. Однако работает это свойство только пока аргумент функции меньше недостижимого кардинала (n < I).
Общее свойство коллапсирования теперь стало следующим:
ψχ(k)(α) = ωΩk+β, где α = k+β – если α > k, k – предельный ординал или ноль.
ψχ(k)(α) = ωΩk+β+1, где α = k+β – если α > k, k – очередной ординал.
ψχ(k)(α) = ωΩα – если α ≤ k, k – предельный ординал или ноль.
ψχ(k)(α) = ωΩα+1 – если α ≤ k, k – очередной ординал.
Бесконечно тетрированный Махло ординал в виде бесконечной степенной башни внутри функции Ратъена, который также можно записать как ψ(εM+1), это особенный ординал, который носит имя Ординал Ратъена.
Майкл и Константин случайно наткнулись на мир, соответствующий этим математическим требованиям.
Майкл и Константин решили отдохнуть от исследований и телепортировались в другое измерение для развлечения. Их приключения начались с первого прыжка в параллельное измерение, где они обнаружили совершенно новые ландшафты и создания. В одном из измерений они оказались в мире, где все предметы обладали живым сознанием. Они познакомились с деревьями, которые могли говорить и дарить свои советы, и с реками, которые имели свои настроения и эмоции. Майкл и Константин провели много времени, изучая этот удивительный мир и узнавая о его уникальных особенностях. Казалось бы, всё отлично, но…
– Если вы одушевлённые, что тогда у вас неодушевлённое? – С интересом спросил Майкл
– Вы имеете ввиду животных? – Поинтересовалось дерево.
– “Животных”?! У вас животные и растения поменялись местами? А что насчёт людей? Вы используете их как стол? – Съязвил Майкл Браун.
– Не, у нас люди крайне многофункциональны, например, из крови мы делаем вино, а вам то это виднее, потому что я очень пьяно. Мне видятся ожившие люди – Сказало дерево решив, что оно словило белочку.
– А этот мир всё-таки криповый, если разобраться – Подметил Константин.
Майкл и Константин решили прогуляться по миру, но все предметы увидев их, резко запаниковали.
– Не с места! А то стрелять буду! – Пригрозил пистолет
– Я думаю, жалкие гномики, которые вылетают из твоего лица, желая принять наше существование близко к сердцу не остановят нас. – С нахальной улыбкой крикнул Константин в ответ.
– Мы вовсе не гномы, дылда ты паранормальная! Мозгов у тебя походу нет, раз ты так высказываешься пистолету при исполнении. А жаль, так хотелось их превратить в вкуснейшую кашицу – Высоким голоском сказала пуля, залезая в дуло пистолета.
Пистолет издал громоподобный выстрел, но сила Константина была настолько могуча, что взмахнув рукой он создал порыв ветра, вернувший пулю обратно в дуло, взорвав живой пистолет на кусочки.
– У меня есть некое подозрение что нам тут не рады, – сказал Майкл и учёные ушли отсюда.
Учёные отправились в почти самый высший нарратив бесконечно малой частицы. И в нём они нашли суперкомпактный (сверхкомпактный) кардинал.
Суперкомпактный кардинал – это концепция из теории множеств, раздела математики, который имеет дело с наборами объектов, называемых множествами. В частности, суперкомпактные кардиналы – это большие кардиналы, которые обладают определёнными свойствами, которые делают их полезными для установления результатов согласованности в рамках теории множеств и для изучения структуры теоретико-множественной вселенной.
Кардинальное число κ считается суперкомпактным, если оно обладает следующим свойством: для любого набора структур {M}, каждая из которых имеет размер меньше, чем κ, и любого унарного предиката (свойства элементов) φ, существует элементарное вложение из вселенной V в более крупную структуру N, такое, что N является структурой размера κ, φ выполняется для элемента из N тогда и только тогда, когда оно выполняется для элемента из V, а критическая точка (наименьший порядковый номер, перемещаемый вложением) меньше, чем κ.
Проще говоря, кардинальное число κ является суперкомпактным, если оно достаточно велико, чтобы любое свойство (описываемое унарным предикатом), которое справедливо для структур меньшего размера, могло быть сохранено и расширено до структуры большего размера κ.
Расширяемый кардинал – это понятие из теории множеств, в частности, из области аксиом большого кардинала. Это утверждения, утверждающие существование определенных видов больших кардинальных чисел с определенными свойствами. Концепция расширяемого кардинала относится к изучению согласованности и структуры математической вселенной, особенно в рамках теории множеств.
Кардинальное число κ считается расширяемым, если существует нетривиальное элементарное вложение j из вселенной V в транзитивную внутреннюю модель M такое, что j (κ) > κ. Здесь "нетривиальный" означает, что вложение не является тождественным отображением, а "элементарное вложение" подразумевает, что вложение сохраняет все утверждения первого порядка о множествах. Проще говоря, расширяемый кардинал κ достаточно велик, чтобы существовал способ "растянуть" универсум за пределы κ значимым образом.