Альтернативой псевдоевклидовому пространству с его метрикой, задаваемой частично через гиперболические функции, а частично через тригонометрические функции, являются координатные системы, в которых длина четырехмерного отрезка определяется только правилами геометрии Евклида. При этом инвариантный интервал определяется в них как длина вектора, исчисляемая с помощью теоремы Пифагора, в соответствии с выражением:

В этом случае мы, при совпадении центров систем координат, имеем дело с использованием только тригонометрических функций для определения геометрии четырехмерных пространств, развернутых на некоторый угол:

И тогда

.

Оба указанных выражения для времени в движущейся системе координат могут быть выведены только с помощью использования факта существования инвариантного интервала, имеющего одну и ту же длину в сравниваемых системах. При этом последнее из них не ограничивает скорость тела скоростью света в вакууме.

Существуют и иные, базирующиеся на понятии об инвариантном времени собственном, способы определения взаимозависимости времен движущейся и неподвижной четырехмерных систем координат, основанные на использовании метода неопределенных коэффициентов (индефинитных преобразований), более известного как преобразования Лоренца ([5], §1):

,

Но и для этих способов применение разных видов инвариантного времени собственного

и , для которых , а , дает те же самые результаты по соотношению хода часов в разных системах координат, что были определены выше и . Как видим, «пространственно-временные» трансляции в результате проведенных преобразований свелись только к временным, а не пространственно- временным трансляциям, как и следовало этого ожидать при принятии условия, что один из наблюдателей видит тело в состоянии покоя (речь конечно же идет о трехмерном пространстве). Причем здесь неподвижной считается система координат, в которой отсутствует движение произвольно выбранной точки в трехмерном подпространстве, но есть движение по временной координате четырехмерного пространства.

Учитывая разночтения в процедуре определения какой из наблюдателей является неподвижным, а какой движущимся, необходимо дополнительно рассмотреть вопрос об определении статуса неподвижности четырехмерных систем отсчета.

Классические преобразования координат, что Галилея, что Лоренца, основаны на сравнении расстояний до произвольно выбранной точки от центров сравниваемых инерциальных систем отсчета. При этом одна из систем координат обязательно должна быть неподвижной относительно указанной точки. Данное обстоятельство позволяет именно в этой системе осуществлять экспериментальную проверку и измерение величины расстояния между указанной точкой и центром системы координат. В другой инерциальной системе координат это расстояние можно вычислить с использованием знания о величине скорости света, величине измеренного в неподвижной системе координат расстояния и скорости относительного движения центров двух систем отсчета. Введение понятия об инвариантном интервале, или времени собственном, как это принято в современной физике, вносит свои коррективы в формулировку ставящейся задачи, поскольку нам необходимо определять не соответствие координат разных систем отсчета, а найти связь между изменениями четырех независимых переменных в разных системах отсчета. При этом мы имеем две четырехмерные системы координат, каждая из которых является неподвижной относительно движущейся произвольно выбранной точки. В одной из систем это движение осуществляется как по временной, так и пространственным координатам, в то время как в другой – только по временной координате. Причем в последней из этих систем движение точки по временной координате согласовано с движением этой же точки по всем четырем координатам в первой из указанных систем отсчета. В общепринятой в настоящее время форме математического обоснования специальной теории относительности для сравнения различных систем координат используют пару идентичных часов, устанавливаемых в центре неподвижной системы координат и на движущемся объекте, полагая, что последние использует наблюдатель, находящийся в системе, где движение тела происходит только по временной координате. Однако такой подход может иметь место только в случае трехмерных, а не четырехмерных систем координат, как это постулируется в специальной теории относительности. В действительности в полном соответствии со специальной теорией относительности мы имеем одни единственные часы, установленные в общем для двух развернутых относительно друг друга четырехмерных систем координат. При этом необходимо ввести условие, что часы в центре системы, где движение тела происходит только по временной координате, показывают то же самое время, что и часы, размещенные в трехмерном пространстве на движущемся теле. Но для описания механического движения тела воспользоваться можно только часами, где это движение осуществляется, то есть в системе, где есть движение по всем координатам четырехмерной системы отсчета. Для часов на наблюдаемом в трехмерном пространстве теле такое движение отсутствует – их показания совпадают с показаниями часов, размещенных в центре системы, где есть движение тела только по временной координате. И для того, чтобы сравнивать показания одних и тех же часов с помощью времени, используемого в трехмерном пространстве, необходимо ввести понятие об инвариантном интервале для различных четырехмерных систем отсчета. При этом базовой (неподвижной) системой может быть только такая, где можно экспериментально определить координатное положение тела и параметры его трехмерного движения. И тогда правомерным следует признать подход к определению статуса неподвижной системы координат, использованный в [5], а не в [8]. В этом случае связь между различными определениями одного и того же четырехмерного инвариантного интервала выражается не через сравнение описаний длины интервала с помощью определения его длины через изменение координат двух четырехмерных систем координат, а через связь для трехмерного пространства между показаниями часов неподвижного наблюдателя и расположенных на движущемся теле часов либо как как

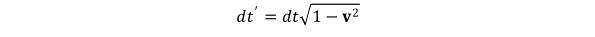
, либо как . Данные выражения легко получить и без рассмотренных ранее математических выкладок, путем простого сравнения метрик (правил определения расстояния между точками) двух различных четырехмерных систем координат, в одной из которых наблюдается движение тела как в трехмерном подпространстве, так и по временной координате, а в другой – только по временной координате. В этом случае на основании инвариантности времени собственного и разных метрик можно записать , c=1. А так как начальным условием является , то . При этом ни о каких иных пространственных преобразованиях не может быть и речи. Более того, при таких видах преобразований построенные нами четырехмерные системы координат будут полностью удовлетворять принципу однородности и изотропности пространства, в то время как именно изотропности пространства одна из систем координат при преобразованиях Лоренца не соответствует.