Итак, мы получили; цифры имеют индивидуальность, качество и порядок, а точки является  определённым местом в пространстве. Следова

тельно: Цифры, своими свойствами, являются первичной реальностью, а точки, вторичная реальность. Но, это в том случае, если цифры и точки являются одним объектом. Далее: (Рис 1, Б): Всякий объект есть целое, состоящее из частей, где каждая часть, в свою очередь может дробиться на более мелкие, но реальные части. В этом случае, каждая часть меньшая по отношению к целому, будет иметь дробное значение. То есть; реальность дроби существует, но целого нет. Так и пишется; 0,1. Ноль, впереди цифры, свидетельствует об отсутствии целого, далее идут части, составляющие целое (1). Ноль, стоящий после цифры, например:10, 20, 100, 3000, свидетельствует об определённом количестве цельного набора реальных объектов; десятки, сотни, тысячи, и так далее. Таким образом, ноль, является носителем информации о дробном или наборе цельных значений реальности!

Следовательно; ноль, это определитель отсутствия, или степени количественного присутствия реальности. Значит; ноль, тоже являются носителем определённой информации

! Далее: Предположим, ряд цифр и точки уходят в бесконечность (Рис 1 Б). Можем ли мы бесконечно считать и изучать реальность? В силу технических и аналитических возможностей, нет! Более того, имеются ограничения по использованию полученных знаний. Это значит, всё, что выше наших возможностей, для нас не имеет смысла и пользы. Тем более, если точки (реальность) закончатся, а цифры можно прибавлять сколько угодно. Таким образом, через отрицательный результат нашего поиска, мы открыли ещё два качества реальности, это смысл и польза! И не случайно! Теперь делаем вывод: Ноль как определяющий фактор информации о реальности, имеет информацию, смысл и пользу. Цифры определяют индивидуальные качества реальных объектов. Реальные объекты, это форма для содержания всех качеств. Форма реальности, это уже вопросы геометрии.

Б). Конструктивная геометрия. Попробуем теоретически, шаг за шагом, методом; «от простого к усложнению», логически раскрыть свойства пространства. Образно выражаясь, возьмём чистый лист бумаги (пространство) и карандаш (замысел). Мы начнём с простого действия, поставим точку (объект) в пространстве (лист бумаги). (Рис 2, а). Далее: Пространство, ничем не

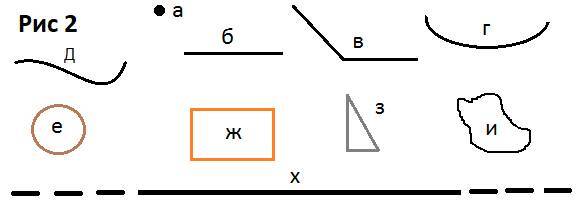
ограничивает объект в формах, содержании и числе (математика). Таким качеством пространства и воспользуемся: Растянем точку в прямую (б), ломанную (в), кривую (г) и волнистую (д) линию. Если точка, является реальным объектом в пространстве, то разные виды линий уже проявляют пространственное качество материи. Используем приобретённое качество материи, соединим концы кривой, ломаных, и волнистых линий, мы получим круг (е), прямоугольник (ж), треугольник (з), и бесформенную фигуру (и). Таким образом, из замкнутых линий получая пространственные фигуры (конструктивная геометрия). Пользуясь безграничностью пространства, теоретически, можем растянуть точку в бесконечную линию (х).

В). Геометрия тел. Используя приобретённый опыт, построим простую объёмную фигуру (Рис 3), А. Поставим точку (г) рядом с треугольником (абв), и соединим точку с углами треугольника. Внутри треугольника, получилось пространство, обозначенное шестью линиями. Для построения куба (Б), можно поставить два квадрата и соединить их вершины линиями. Таким методом можно построить много разнообразных, объёмных фигур. Заметим: Объём обозначенный линиями, так и остался частью пространства.

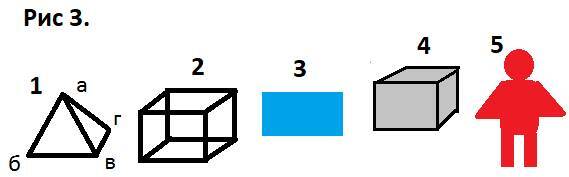
Г). Свойства тел. По сторонам линий фигур, расширим линии до полноты внутреннего пространства. Линии перешли в грани (границы), плоской фигуры и мы получили новое качество материи; плоскость (3). Плоскость, как и линии, имеют материальную плотность (насыщенность). На следующем этапе, из плоскостей, построим объёмную фигуру, например куб (4). Таким образом, внутри куба, останется изолированная часть пространства (пустота), с такими же свойствами, как и внешнее пространство. Здесь можно говорить о форме (границы), и содержании (внутреннее пространство). Следующий этап: Увеличиваем толщину плоскостей объёмной фигуры (4) вовнутрь, до полного заполнения пустоты. На этом этапе получим цельную фигуру, приобретая массу тела. Соединяя формы разных фигур (5), можно создать разные комбинации форм, с разным или одинаковым содержанием (масса, плотность). Таким образом, мы получили объекты в пространстве со своими границами и свойствами.

Геометрия

мира: 1.Точка. 2. Прямая линия. 3. Пунктирная линия. 4. Ломаная линия (угол). 5. Кривая (дуга). 6. Замкнутая линия (плоскость). 7.Куб, шар. (Объём).8. Содержание объёма (качество). У качества, как мы уже выяснили, есть смысл. Таким образом: Формы мира имеют свойства, содержание форм, имеют смысл. При этом надо иметь в виду, границы и свойства фигур, результат использования пространства. Следовательно: Пространство не пустое, имеет свойства в виде информации, качества, смысла и пользы. Пространство, производное разнообразных форм реальности. Усложним, полученные результаты.

Д). Связь. В этом варианте (рис 4), поставим Наблюдателя, Наблюдатель (Н) находится на одной линии с телами (АБВ), и угловым зрением видит тело (А), но не видит тел (БВ). Тела (Б и В), больше тела (А), но для Наблюдателя (Н), являются скрытой реальностью. Более того, из рисунка видно, что угловым зрением не определить истинные размеры тела, и его удалённость от Наблюдателя.

Тело малого размера на месте (А), тело большого размера удалённого на место тела (В), угол зрения наблюдателя не изменят. Для устранения недостатка, поставим второго Наблюдателя в точке (Н 2).

Наблюдатель 2, может определить число тел, но их размеры и удалённость от себя не определит по те

м -

же причинам, что и первый наблюдатель. Для полного решения задачи, наблюдателям необходим обмен информацией (И) о телах (связь), и о своём месте нахождения (Л). Для этого, пространство должно иметь способность передавать информацию. Это значит, что наблюдатели видят друг друга, и способны вместе анализировать ситуацию (Мысль). Разные точки наблюдения за объектами, с целью определения их положения в пространстве, по сути, являются Системой Координат.

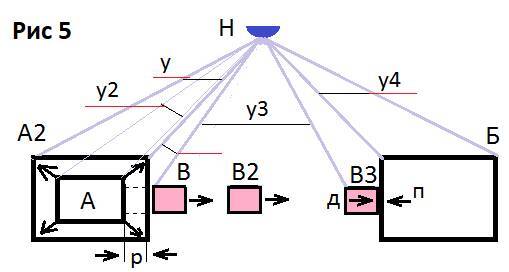
Е). Действия тел. Рис 5. На рисунке три тела; А, Б, В. Тело (А) увеличиваем в размерах до размера (А 2). Расширяясь, тело (А) окажет давление на тело (В). Тело (В) сохраняя свою форму, начнёт совершать движение (принудительное перемещение). В конечной точке роста тела (А 2), сила давления закончится, тело (В) получив толчок, не встречая сопротивление, продолжит передвижение в пространстве (инерция). Инерция (в данном случае), это сохранённая сила давления (память)! Тоесть, один вид энергии (давление) перешёл в другой вид энергии (инерция). Далее: Когда тело (В) достигнет тела (Б), сила инерции переходит в силу удара (столкновение).

Масса тела (Б) превышает массу тела (В) и по условию эксперимента, остаётся на месте. В месте соприкосновения тел, возникнет равноценная сила ответного удара (сила противодействия) на тело (В), и тело начнёт обратное перемещение (отскок) к телу (А). Плотность тела (Б) сохраняет геометрию (форму) тела, а масса, сохраняет неподвижность в пространстве (память покоя). Можно и так сказать: Инерция (динамическая память толчка), столкнулась с памятью покоя (статическая сила). Итак: «Инерция, это память физического воздействия тел». Столкновение с телом (А), по тем же причинам, приведёт к перемещению тела (В) к телу (Б), и всё повторится. Таким образом, получится маятниковое движение тела (В) с изменением видов энергии. Для определения действий, поставим Наблюдателя (Н). Наблюдатель по углам зрения (у), определит наличие и количество тел (Информация). Наблюдатель будет получать новые данные об изменении объёма тела (А), но для определения его роста, надо помнить его предыдущий размер. Следовательно, Наблюдатель обладает памятью, и способностью к анализу изменяемой ситуации. Наблюдатель, обладая памятью и способностью к анализу изменений, зафиксирует движение тела (В). Заметим: Место для наблюдения Выбрано Целенаправленно на равном удалении от тел (А и Б). Значит, выбор имеет Смысловое и Волевое действие! Оставим пока вопрос о природе угла зрения открытым.