Теперь посмотрим, как будет выглядеть сигнал, изображенный на рис. 2.1, а, если полоса пропускания канала будет такой, что через него будут проходить только самые низкие частоты (то есть функция g(t) будет аппроксимирована лишь несколькими первыми членами рядов выражения (2.1)). На рис. 2.1, б показан сигнал на выходе канала, пропускающего лишь первую (основную, f) гармонику сигнала. Аналогично, рис. 2.1, в-д показывают спектры и восстановленные сигналы для каналов с более широкой полосой пропускания. Что касается цифровых данных, то главная задача — передавать их с минимальным качеством, позволяющим восстановить первоначальную последовательность битов. Для этого достаточно сигнала, показанного на рис. 2.1, д; следовательно, совершенно не нужно тратить ресурсы и использовать большее количество гармоник для получения более точной копии.
При заданной скорости передачи в битах, равной b бит/с, время, требуемое для передачи, скажем, 8 бит, будет равно 8/b секунд. Таким образом, частота первой гармоники равна b/8 Гц. Обычная телефонная линия, часто называемая речевым каналом, имеет искусственно созданную частоту среза около 3000 Гц. Это ограничение означает, что номер самой высокой гармоники, прошедшей сквозь телефонный канал, примерно (срез не очень крутой) равен 3000/(b/8) или 24 000/b.
Для некоторых скоростей передачи данных эти значения показаны в табл. 2.1. Из приведенных данных ясно, что попытка передать по речевому каналу данные на скорости 9600 бит/с превратит сигнал, показанный на рис. 2.1, а, в нечто подобное рис. 2.1, в, что сделает прием исходного потока битов с приемлемым качеством практически невозможным. Очевидно, что у сигналов, передаваемых со скоростью 38 400 бит/с и выше, нет никаких шансов пройти через речевой канал, даже при полном отсутствии
помех на линии. Другими словами, ограничение полосы пропускания частот канала ограничивает его пропускную способность для передачи двоичных данных даже для идеальных каналов. Однако схемы, использующие несколько уровней напряжений, существуют и позволяют достичь более высоких скоростей передачи данных. Мы обсудим это ниже в этой главе.
Таблица 2.1. Соотношение между скоростью передачи данных и числом гармоник для нашего примера
Бит/с T, мс 1-я гармоника, Гц Количество пропускаемых гармоник
300
26,67
37,5
80
600
13,33
75
40
1200
6,67
150
20
2400
3,33
300
10
4800
1,67
600
5
9600
0,83
1200
2
19 200
0,42
2400
1
38 400
0,21
4800
0
С термином «полоса пропускания» связано множество недоразумений, так как для инженеров-электриков и компьютерных специалистов он означает разные вещи. Для инженера-электрика (аналоговая) полоса пропускания, как уже говорилось выше, это значение в герцах, указывающее ширину диапазона частот. Для компьютерного специалиста (цифровая) полоса пропускания — это максимальная скорость данных в канале, то есть значение, измеряемое в битах в секунду. Фактически скорость данных определяется аналоговой полосой пропускания физического канала, применяемого для передачи цифровой информации, и эти два показателя связаны, как мы увидим далее. В этой книге будет понятно из контекста, какой термин имеется в виду в каждом конкретном случае — аналоговая (Гц) или цифровая (бит/с) полоса пропускания.
2.1.3. Максимальная скорость передачи данных через канал
В 1924 году американский ученый Х. Найквист (H. Nyquist) из компании AT&T пришел к выводу, что существует некая предельная скорость передачи даже для идеальных каналов. Он вывел уравнение, позволяющее найти максимальную скорость передачи данных в бесшумном канале с ограниченной полосой пропускания частот. В 1948 году Клод Шеннон (Claude Shannon) продолжил работу Найквиста и расширил ее для случая канала со случайным (то есть термодинамическим) шумом. Это важнейшая работа во всей теории передачи информации. Мы кратко рассмотрим результаты работы Найквиста и Шеннона, ставшие сегодня классическими.
Найквист доказал, что если произвольный сигнал прошел через низкочастотный фильтр с полосой пропускания B, то такой отфильтрованный сигнал может быть полностью восстановлен по дискретным значениям этого сигнала, измеренным с частотой 2B в секунду. Производить измерения сигнала чаще, чем 2B в секунду, нет смысла, так как более высокочастотные компоненты сигнала были отфильтрованы. Если сигнал состоит из V дискретных уровней, то уравнение Найквиста будет выглядеть так:
Так, например, бесшумный канал с частотой пропускания в 3 кГц не может передавать двоичные (то есть двухуровневые) сигналы на скорости, превосходящей 6000 бит/с.
Итак, мы рассмотрели случай бесшумных каналов. При наличии в канале случайного шума ситуация резко ухудшается. Уровень термодинамического шума в канале измеряется отношением мощности сигнала к мощности шума и называется отношением сигнал/шум. Если обозначить мощность сигнала S, а мощность шума — N, то отношение сигнал/шум будет равно S/N. Обычно величина отношения выражается через ее десятичный логарифм, умноженный на 10: 10 lg S/N, так как ее значение может меняться в очень большом диапазоне. Единица такой логарифмической шкалы называется децибелом (decibel, dB, дБ); здесь приставка «деци» означает «десять», а «бел» — это единица измерения, названная в честь изобретателя телефона Александра Грэма Белла. Таким образом, отношение сигнал/шум, равное 10, соответствует 10 дБ, отношение, равное 100, равно 20 дБ, отношение, равное 1000, равно 30 дБ и т. д. Производители стереоусилителей часто указывают полосу частот (частотный диапазон), в которой их аппаратура имеет линейную амплитудно-частотную характеристику в пределах 3 дБ. Отклонение в 3 дБ соответствует ослаблению сигнала примерно в два раза
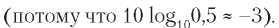
Главным результатом, который получил Шеннон, было утверждение о том, что максимальная скорость передачи данных или емкость канала с полосой частот B Гц и отношением сигнал/шум, равным S/N, вычисляется по формуле:
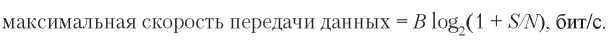
Это наилучшее значение емкости, которое можно наблюдать для реального канала. Например, полоса пропускания канала ADSL (Asymmetric Digital Subscriber Line, ассиметричная цифровая абонентская линия), по которому осуществляется доступ в Интернет через телефонные сети, равна приблизительно 1 МГц. Отношение сигнал/ шум в значительной степени зависит от расстояния между компьютером пользователя и телефонной станцией. Для коротких линий длиной от 1 до 2 км очень хорошим считается значение около 40 дБ. С такими характеристиками канал никогда не сможет передавать более 13 Мбит/с, независимо от способа модуляции сигнала, то есть количества используемых уровней сигнала, частоты дискретизации и т. д. Поставщики услуг заявляют скорость передачи данных до 12 Мбит/с, однако пользователям редко удается наблюдать такое качество передачи данных. Тем не менее это великолепный результат для шестидесяти лет развития технологий передачи информации, в течение которых произошел огромный скачок от емкости каналов, характерной для времен Шеннона, и до существующей в современных реальных сетях.
Результат, полученный Шенноном и подкрепленный постулатами теории информации, применим к любому каналу с Гауссовским (термальным) шумом. Попытки доказать обратное заранее обречены на провал. Для того чтобы добиться в канале ADSL скорости, превышающей 13 Мбит/с, необходимо либо улучшить отношение
сигнал/шум (например, добавив цифровые повторители в линии передачи данных, подходящие к компьютерам пользователей), либо расширить полосу пропускания, как это сделано в новой версии технологии, ADSL2+.