Итак, новый протокол аутентификации показан на рис. 8.32 (Bird и др., 1993). Тут мы видим тот же самый HMAC, который мы уже обсуждали при изучении IPsec. Для начала Алиса посылает Бобу nonce R_A в виде сообщения 1. Боб при ответе выбирает собственную nonce, R_B, и высылает ее вместе с HMAC. HMAC формируется построением структуры данных, состоящую из nonce Алисы и Боба, их идентификаторов, а также общего закрытого ключа K_AB. Затем вся эта структура с помощью хэш-функции (например, SHA-1) помещается в HMAC. После приема сообщения 2 Алиса становится счастливым обладателем R_A (это значение выбрано ею же), R_B, полученного в виде открытого текста, двух идентификаторов и закрытого ключа K_AB, известного и так. Имея все эти данные, она может вычислить HMAC самостоятельно. Если он согласуется с HMAC, содержащимся в сообщении, она убеждается, что говорит с Бобом, поскольку Труди не знает K_AB и, следовательно, не может угадать HMAC, который следует отослать. В ответе Алисы Бобу содержится HMAC, состоящий из двух nonce.

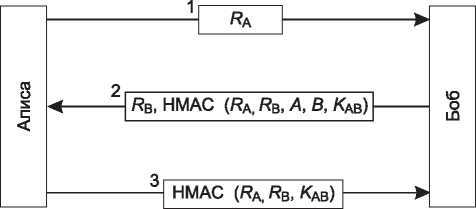
Вопрос: может ли Труди как-нибудь взломать такой протокол? Нет, потому что она не может заставить ни одну из сторон шифровать выбранное ей самой значение или применять к нему хэш-функцию, как это было в ситуации на рис. 8.30. Оба HMAC включают в себя значения, выбранные отправителем. Труди не способна их контролировать каким-либо образом.

Использование HMAC — это далеко не единственное, что можно сделать. Альтернативная схема, которая применяется довольно часто, заключается в шифровании элементов данных последовательно с помощью сцепления блоков шифра.

8.7.2. Установка общего ключа: протокол обмена ключами Диффи—Хеллмана

Итак, мы предположили, что у Алисы и Боба есть общий секретный ключ. Предположим теперь, что у них его нет (поскольку до сих пор не разработана универсальная инфраструктура PKI создания подписей и распространения сертификатов). Как им получить такой ключ? Алиса может позвонить Бобу и передать ему ключ по телефону, но он, возможно, спросит: «Как вы докажете, что вы — Алиса, а не злоумышленник?» Они могут попытаться организовать встречу, на которую каждый придет с паспортом, водительскими правами и тремя кредитными картами, но, будучи занятыми людьми, они, возможно, не смогут найти устраивающую обоих дату встречи в течение нескольких месяцев. К счастью, существует способ для совершенно незнакомых людей установить общий секретный ключ среди бела дня, даже если злоумышленник старательно записывает каждое сообщение.

Протокол, позволяющий не встречавшимся ранее людям устанавливать общий секретный ключ, называется протоколом обмена ключами Диффи—Хеллмана (Diffie—

Hellman key exchange) (Diffie и Hellman, 1976) и работает следующим образом. Алиса и Боб договариваются о двух больших простых числах, n и g, где (n-1)/2 — также является простым числом, кроме того, на число g накладываются некоторые дополнительные условия. Эти числа могут быть открытыми, поэтому каждый из них может просто выбрать n и g и открыто сообщить о них другому. Затем Алиса выбирает большое (например, двоичное 1024-разрядное) число x и держит его в секрете. Аналогично, Боб выбирает большое секретное число у.

Алиса начинаетпротокол обмена ключами с того, что посылает Бобу сообщение, содержащее

как показано на рис. 8.33. Боб отвечает Алисе сообщением,

содержащим gy mod n. Теперь Алиса берет число, присланное ей Бобом, и возводит его в степень x, получая

Боб выполняет подобные вычисления,

и получает

В соответствии с законами модульной арифметики оба

вычисления должны быть равны g^xy mod n. Таким образом, как по мановению волшебной палочки, у Алисы и Боба есть общий секретный ключ

Конечно, злоумышленник видел оба сообщения. Ему известны значения n и g из первого сообщения. Если бы ему удалось вычислить значения x и у, ему бы удалось получить секретный ключ. Беда в том, что, зная g^x mod n и n, найти значение x очень трудно. На сегодняшний день неизвестен алгоритм вычисления дискретного логарифма модуля очень большого простого числа.

Для примера возьмем (совершенно нереальные) значения n = 47 и g = 3. Алиса выбирает значение x = 8, а Боб выбирает у = 10. Оба эти числа хранятся в секрете. Со-

общение Алисы Бобу содержит числа (47, 3, 28), так как 3⁸ mod 47 = 28. Боб отвечает Алисе числом 17. Алиса вычисляет 17⁸ mod 47 и получает 4. Боб вычисляет 28¹⁰ mod 47 и получает также 4. Таким образом, независимо друг от друга, Алиса и Боб определили, что значение секретного ключа равно 4. Чтобы найти ключ, злоумышленнику придется решить уравнение 3^х mod 47 = 28, что можно сделать путем полного перебора для таких небольших чисел, но только не для чисел длиной в несколько сотен бит. Все известные в настоящее время алгоритмы просто очень долго работают, даже на работающих параллельно наибыстрейших суперкомпьютерах.

Рис. 8.33. Протокол обмена ключами Диффи—Хеллмана

Несмотря на всю элегантность алгоритма Диффи—Хеллмана, имеется одна проблема: когда Боб получит три числа (47, 3, 28), как он сможет удостовериться в том, что они посланы Алисой, а не злоумышленником (Труди)? Способа узнать это не существует. К сожалению, Труди может воспользоваться этим, чтобы обмануть Алису и Боба, как показано на рис. 8.34. Здесь, пока Алиса с Бобом выбирают значения x и у, Труди выбирает свое случайное число z. Алиса посылает Бобу сообщение 1. Труди перехватывает его и отправляет вместо него Бобу сообщение 2, используя правильные значения n и g (которые посылались открытым текстом), но со своим значением z вместо х. Она также посылает обратно Алисе сообщение 3. Позднее Боб отправляет Алисе сообщение 4, которое Труди снова перехватывает и хранит у себя.

Рис 8.34. Атака типа «человек посередине»

Теперь все занимаются вычислением остатков от деления. Алиса вычисляет значение секретного ключа: g^xz mod n. Те же самые вычисления производит Труди (для общения с Алисой). Боб вычисляет g^yz mod n, что также делает и Труди (для общения с Бобом). Каждое сообщение, посылаемое Алисой в шифрованном сеансе, перехватывается Труди, сохраняется, изменяется, если это нужно, и отправляется (по желанию

Труди) Бобу. То же самое происходит и в обратном направлении. Труди видит все сообщения и может изменять их по своему усмотрению, в то время как Алиса и Боб полагают, что у них имеется защищенный канал для связи друг с другом. Подобные действия злоумышленника называются атакой типа «человек посередине» (man-in-the-middle attack). Еще одно название этой атаки — «пожарная цепочка» (bucket brigade attack), поскольку слегка напоминает старинных пожарных, передававших друг другу по цепочке ведра с водой.

8.7.3. Аутентификация с помощью центра распространения ключей

Итак, установка общего секретного ключа с незнакомцем почти удалась. С другой стороны, вероятно, не следовало вообще этим заниматься. Чтобы общаться с n людьми, вам понадобится хранить n ключей. Для людей, чей круг общения широк, хранение ключей может превратиться в серьезную проблему, особенно если все эти ключи придется хранить на отдельных пластиковых картах.