Все вышесказанное свидетельствует о кажущейся «непрактичности» космологии как физической дисциплины. Цель данной работы – опровержение этого утверждения. Мы попытаемся показать, что справедливо прямо обратное суждение: космология является самой практической из всех наук, поскольку, как мы увидим, приводит к выводам, весьма актуальным не только для космологов, но и для всех людей, в том числе далеких от науки. Мы покажем, что если так называемая стандартная космологическая модель (СКМ), о которой иногда говорят как о «космологическом коркодансе», верна, то человеческой цивилизации осталось существовать гораздо меньше, чем это принято думать! Насколько меньше? Речь идет не о миллионах или тысячах лет, а о столетиях или даже, при наиболее экзотичном варианте, десятилетиях! Вероятно, читатель подумает, что авторы занимаются мистификацией. Каким образом изучение вселенной как целого может привести к таким выводам? Поразительно, но может. Именно этой теме посвящена данная работа. Отметим, что предсказания о грядущем «конце света», сделанные на основе чисто статистических аргументов, давно и оживленно обсуждаются в литературе. Появился специальный термин: Аргумент Судного дня (в подлиннике Doomsday argument [Carter, 1983; Leslie, 1990; Gott, 1993; Nielsen, 1989]). Аргумент Doomsday не использовал космологических соображений и подвергался обширной критике. Наиболее ясно эта позиция изложена в статье Олума [Olum, 2002]. Мы, однако, покажем, что критика Олума несправедлива, если принять во внимание СКМ. Более точно, используя аргументацию Олума в рамках «космологического коркоданса», мы неизбежно приходим к справедливости Аргумента Doomsday. Другими словами, Кен Олум доказал справедливость Аргумента Судного дня, хотя и написал свою работу с целью опровержения последнего!

Работа организована следующим образом: во втором разделе мы обсуждаем Аргумент Судного дня и решение, предложенное Олумом для устранения последнего. В третьем разделе мы показываем, что правило подсчета частот в мультиверсе отличается от того, которое использовалось в [Olum, 2002] для решения парадокса Doomsday и, напротив, приводит к справедливости Аргумента Судного дня. В четвертом разделе, используя данные математической демографии и методы, развитые выше, мы оцениваем время наступления «конца света». Даже грубые вычисления свидетельствуют о том, что «конец света» должен наступить в течение ближайших десятилетий. Трудно счесть такое заключение чем‐то непрактичным, не так ли?

В своей классической постановке Аргумент Doomsday выглядит следующим образом: пусть p_S и p_L  – вероятности того, что человеческая цивилизация (раса) будет существовать соответственно «недолго» и «долго». Срок существования – не определяется. Все, что нам надо знать, – это то, что в первом случае человечество исчезнет, набрав в «общей сумме» N_S когда-либо живших людей, а во втором – N_L, причем N_L >> N_S. Разумеется, эта картина может показаться чрезвычайно упрощенной. Наверное, возможно множество вариантов развития человечества, и нелепо все сводить к двум возможностям. Тем не менее в качестве некоей усредненной картины ее использовать можно. Современный уровень знаний не позволяет вычислить числа p_S и p_L = 1− p_S, но этого и не требуется. Более того, можно даже принять оптимистичный взгляд на вещи и считать, что величина p_L по крайней мере не меньше величины p_S. Это не изменит конечного результата. Нас будет интересовать условная вероятность p (S|N), которая равна вероятности того, что «я» живу в короткоживущей цивилизации, при условии, что я N-й рожденный человек. Конечно, определить величину N – затруднительно, поскольку непонятно кого считать первым человеком. Но в принципе ясно, что какое бы соглашение относительно первого человека ни было принято, в рамках его число N будет определено.

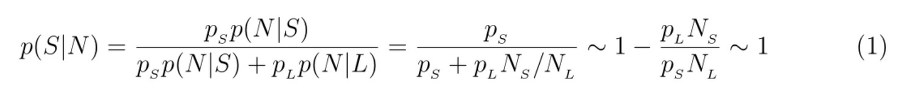
Пусть p (N|S) и p (N|L) условные вероятности того, что я N-й рожденный человек в, соответственно, короткоживущей и долгоживущей расах. Очевидно p (N|S)/p (N|L) = N_L/N_S. Используя формулу Байеса, находим результат, так как N_S/N_L << 1. Таким образом, условная вероятность найти себя в короткоживущей расе неожиданно оказывается порядка единицы! Это и есть знаменитый Аргумент Doomsday.

A. Аргумент Doomsday содержит внутреннее противоречие. Представим себе, что несколько десятков тысяч лет назад численность народонаселения составляла в общей сумме (вместе с умершими) 1000 человек. Предположим, что эти люди – фаталисты, уверенные, что грядет конец света, и оценивают общее число всех людей своей расы, вплоть до этого конца в 10⁶. Как мы знаем, сейчас число всех когда-либо живших людей составляет около 60 млрд человек5. Примем, что p_S = p_L = 0,5. Тогда формула (1) дает

Другими словами, фактически со 100%-ной гарантией эти люди должны были оказаться правы в своих апокалиптических ожиданиях. Вероятность же текущего положения дел (на начало XXI в.) составила бы лишь 0,000017. Тем не менее, как мы знаем, именно это практически невероятное состояние человечества имеет место. Таким образом, древние люди совершили бы огромную ошибку, полагаясь на формулу (1). Но тогда почему мы должны доверять этой формуле?

B. Аргумент Doomsday дает заведомо неправильный ответ. Здравый смысл подсказывает, что вероятность p (S|N) должна быть равна просто p_S. Очевидно, где‐то имеется ошибка в вычислениях.

Кен Олум утверждает, что знает где. Вот его рассуждения: для нахождения условной вероятности p (S|N) мы перемножили два числа (опуская нормировочный множитель):

тогда как правильное выражение имеет вид

Вводя в (4) нормировочный множитель, имеем

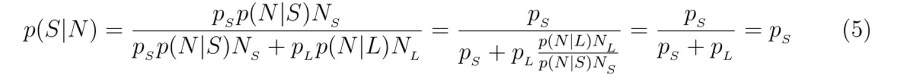
Ответ получается разумным, но почему нам следует использовать предписание (4), а не (3)? Согласно Олуму, для правильного вычисления p (S|N) необходимо перемножить три вероятности: вероятность того, что мы находимся в короткоживущей цивилизации (p S), условную вероятность того, что я N-й человек (p (N|S)), и p (N_S|I) – условную вероятность того, что я нахожусь в короткоживущей цивилизации, при условии, что «я есть». Последнее выглядит странно и нуждается в пояснении. Суть дела в том, что сам факт моего существования служит аргументом в пользу того, что я нахожусь в долгоживущей цивилизации, насчитывающей большое число людей. Другими словами, вероятность p (N_S|I) должна быть пропорциональна полному числу людей – N_S. Для того чтобы сделать этот вопрос максимально ясным, рассмотрим (вслед за Кен Олумом) следующую гипотетическую игровую ситуацию. Пусть некое высшее существо (Олум называет ее богиней) имеет в запасе отель, содержащий 10⁹ одноместных номеров и такое же число людей (одним из которых являюсь я). Богиня бросает монету и в зависимости от того, что выпадает – «орел» или «решка», реализует следующую стратегию.

Стратегия 1.

1.1. Если выпадает «орел», то богиня случайным образом расселяет всех 10⁹ человек по номерам.

1.2. Если выпадает «решка», то богиня случайным образом выбирает 10 человек и наугад расселяет их по первым 10 номерам.

Предположим, что я обнаружил, что нахожусь в одном из первых 10 номеров. С какой вероятностью у богини выпал «орел»? Или иначе, какова вероятность того, что отель полон людей? Эти вопросы имеют прямое отношение к Аргументу Doomsday. В самом деле, результат, полученный по формуле (1), можно объяснить и так: если человечество будет существовать очень долго и полное число всех людей (N_L) будет очень велико, то кажется весьма маловероятным найти себя в малой доле людей, живущих у истока цивилизации. Однако мы находим себя в нем, значит, полное число всех когда-либо живших людей, людей, живущих сейчас, и тех, кто будет жить после, не должно быть очень велико. Формула (1) просто дает количественное основание этой идеи. Аналогично в мысленном эксперименте Кен Олума кажется весьма маловероятным, что отель полон, коль скоро мы нашли себя уже в первой десятке номеров. Однако это интуитивно очевидное заключение оказывается неверным. Назовем группу людей, которых богиня будет расселять по номерам реферируемой группой. Теперь предположим, что монета упала «орлом». В этом случае с вероятностью единицы я окажусь в реферируемой группе. Вероятность же того, что богиня поместит меня в один из первых десяти номеров, составит 10⁻⁸. Перемножая эти независимые вероятности, я получаю вероятность попасть в первые десять номеров при выпадении «орла», равной 10⁻⁸. Если же монета упадет «решкой», то мои шансы попасть в реферируемую группу составят десять к миллиарду, зато вероятность того, что я окажусь в первой десятке номеров, равна, очевидно, 1. Перемножая эти числа, получаем ту же вероятность 10⁻⁸, что и при выпадении монеты «орлом». Заметим, что вероятность моего попадания в реферируемую группу и есть величина p (N_S|I) (или p (N_S|I)). Отношение этих вероятностей в первом и втором случаях составляет один к 10⁻⁸, т.е. равно отношению числа членов в реферируемых группах: 10⁹ к 10. Именно поэтому p (N_S|I) ∼ N_S, а p (N_L|I) ∼ N_L. Таким образом, вероятность моего попадания в номер, скажем, 7 не зависит от числа людей в отеле и составляет, очевидно, 10^–9. В свою очередь это означает, что вероятности выпадения монеты «орлом» или «решкой» равны, а значит, вероятность того, что отель полон, равна 1/2, т.е., возвращаясь к Аргументу Doomsday, p (S|N) = p_S. Таким образом, парадокс Судного дня кажется решенным. Но не все так просто!