Такие рассуждения привели Ньютона к предположению о том, что каждое тело во Вселенной притягивает к себе все остальные тела. Законы Кеплера приложимы только к двум телам – Солнцу и планете. Закон Ньютона применим к любой системе тел в принципе, поскольку он дает как величину, так и направление всех возникающих в системе сил. При подстановке в законы движения комбинация всех этих сил определяет ускорение каждого тела и, следовательно, его скорость и положение в любой момент времени. Провозглашение универсального закона гравитации стало эпохальным событием в истории науки – событием, которое позволило прояснить скрытый математический механизм, обеспечивающий существование Вселенной.

Ньютоновы законы движения и гравитации положили начало долговременному союзу между астрономией и математикой – союзу, которому мы обязаны значительной частью того, что знаем сегодня о космосе. Но даже если вы поняли, что представляют собой эти законы, то это не значит, что вы сможете напрямую применить их к решению конкретных задач. Сила тяготения, к примеру, нелинейна – этот технический термин означает, в сущности, что вы не можете решать уравнения движения при помощи красивых формул. И при помощи некрасивых, кстати говоря, тоже.

Математики постньютоновской эпохи обходили это препятствие двумя способами: либо разбирали совершенно искусственные (хотя и очень интересные) задачи, такие, например, как взаимодействие трех одинаковых масс, расположенных в вершинах равностороннего треугольника, либо искали приближенные решения более реалистичных задач. Второй подход более практичен, но следует отметить, что немало полезных идей удалось извлечь именно из первого подхода, несмотря на всю его искусственность.

На протяжении долгого времени научным наследникам Ньютона приходилось производить все вычисления вручную – и во многих случаях это была поистине героическая задача. Яркий пример такого рода – Шарль-Эжен Делоне, который в 1846 году начал вычислять приближенную формулу движения Луны. На это у него ушло более двадцати лет, а результаты пришлось публиковать в двух томах. В каждом из этих томов более 900 страниц, и весь второй том занимает собственно формула. В конце XX века результат Делоне удалось проверить с применением компьютерной алгебры (программных систем, способных манипулировать не только числами, но и формулами). Было выявлено всего две небольшие ошибки, одна из которых является следствием другой; суммарный эффект от обеих ошибок пренебрежимо мал.

Законы движения и гравитации – это законы особого рода, законы, выражаемые так называемыми дифференциальными уравнениями. Такие уравнения задают скорость, с которой те или иные величины изменяются с течением времени. Скорость – это быстрота изменения положения тела; ускорение – это быстрота изменения скорости. Знание скорости, с которой в настоящее время изменяется та или иная величина, позволяет вам спроецировать эту величину в будущее. Если машина едет со скоростью 10 метров в секунду, то через секунду она сдвинется на 10 метров. Однако для того, чтобы считать таким способом, нужно, чтобы скорость была постоянной. Если же машина ускоряется, то за секунду она отъедет от вас более чем на 10 метров. Чтобы обойти эту проблему, в дифференциальных уравнениях указывается мгновенная быстрота изменения. По существу, они работают с очень короткими промежутками времени, так что быстроту изменения на этом промежутке можно считать постоянной. На самом деле математикам потребовалось несколько столетий, чтобы довести эту идею до полной логической строгости, поскольку никакой конечный интервал времени нельзя считать мгновенным, если он не равен нулю, а за нулевой интервал времени ничто не меняется.

Компьютеры произвели в этом деле настоящую методологическую революцию. Вместо расчета приближенных формул движения, а затем подстановки чисел в эти формулы теперь можно с самого начала работать с числами. Предположим, вы хотите предсказать, где некоторая система тел – скажем, спутники Юпитера – будет находиться через сто лет. Начните с первоначальных позиций и параметров движения Юпитера, его спутников и всех остальных тел, которые могут иметь значение, – в данном случае это Солнце и Сатурн. Затем, постепенно, один крошечный временной шаг за другим, вычисляйте, как изменяются числа, описывающие все задействованные тела. Повторяйте это действие до тех пор, пока не дойдете до временной отметки сто лет. Стоп. Человек, проводящий вычисления при помощи карандаша и бумаги, не смог бы воспользоваться этим методом для расчета сколько-нибудь реалистичной задачи. На это потребовалось бы несколько жизней. Однако при наличии быстрого компьютера метод становится вполне реализуемым, а современные компьютеры очень и очень быстры.

Откровенно говоря, все не настолько просто. Притом что ошибка на каждом шаге (вызванная тем, что мы считаем быстроту изменений постоянной, хотя на самом деле она успевает немного измениться) очень мала, шагов вам придется сделать ужасно много. При многократных операциях с маленькой ошибкой на каждом шагу результирующая ошибка не обязательно получится маленькой, но тщательно продуманные методы позволяют удержать ошибки под контролем. Именно на это нацелена целая область математики, известная как численный анализ. Удобно называть такие методы «моделированием», что отражает принципиальную роль в них компьютера. Важно понимать, что невозможно решить задачу, просто «засунув ее в компьютер». Кто-то должен запрограммировать машину, задать ей математические правила, которые обеспечат близость вычислительных результатов к реальности.

Правила, о которых идет речь, настолько точны, что астрономы могут предсказывать затмения Солнца и Луны с точностью до секунды, а положение планеты с точностью до нескольких километров на сотни лет вперед. Подобные «предсказательные» расчеты можно проводить и назад во времени, чтобы можно было точно определить, когда и где произошли известные нам по историческим хроникам затмения. Эти данные используются, к примеру, для датирования наблюдений, сделанных тысячи лет назад китайскими астрономами.

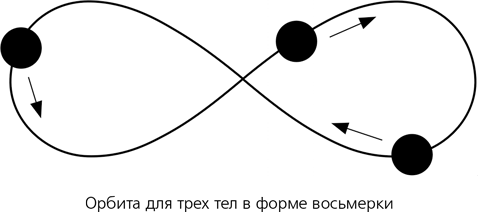
Даже сегодня математики и физики продолжают открывать новые неожиданные следствия из закона всемирного тяготения Ньютона. В 1993 году Крис Мур при помощи численных методов показал, что три тела с идентичными массами могут вечно гоняться друг за другом по одной и той же орбите в форме восьмерки, а в 2000-м Карлес Симо также численно показал, что эта орбита стабильна с точностью, возможно, до медленного дрейфа. В 2001 году Ален Ченсинер и Ричард Монтгомери привели строгое доказательство существования такой орбиты на основе принципа наименьшего действия – фундаментальной теоремы классической механики. Симо открыл множество подобных «хореографий», в которых несколько тел одинаковой массы преследуют друг друга, двигаясь все время по одному и тому же (сложному) пути.

Орбита в форме восьмерки для трех тел, судя по всему, сохраняет стабильность и при слегка различных массах тел, что открывает небольшую вероятность того, что где-то во Вселенной три реальные звезды могут вести себя таким замечательным образом. Согласно оценкам Дугласа Хегги, по одной такой тройной системе может приходиться на каждую галактику, а уж вероятность существования во Вселенной хотя бы одной такой системы довольно значительна.

Все эти орбиты существуют на плоскости, но есть уже и новый трехмерный вариант. В 2015 году Юджин Окс догадался, что необычные орбиты электронов в «ридберговских квазимолекулах», возможно, тоже существуют по законам Ньютоновой гравитации. Он показал, что в системах двойных звезд могут существовать планеты, двигающиеся от одной звезды к другой и обратно по спиральной орбите, обвивающей соединяющую эти звезды линию. В середине витки спирали лежат свободнее, к звездам на концах – плотнее. Представьте себе, что вы протягиваете между звездами пружинку игрушку-слинки, растянутую посередине и свернутую в петли на концах. Для звезд с разными массами пружинка должна сужаться от одного конца к другому, как конус. Подобные орбиты могут быть стабильными, даже если звезды движутся не по окружностям.