Рис. 18. Наблюдатель S в Солнечной системе будет видеть больше звёзд по любому направлению Sx, лежащему в плоскости галактического диска, чем в перпендикулярном направлении Sy (а). Галактика похожа на диск с центральным утолщением. Солнце (°) находится на расстоянии, приблизительно равном 2/3 расстояния от центра до края (б)
Этот диск, видимый изнутри, проектируется на небесную сферу (т.е. на ночное небо) в виде полосы.
Таким образом, наблюдение Млечного Пути указывает на то, что мы находимся внутри дискообразного распределения звёзд. Более внимательные наблюдения звёзд в разных направлениях приводят к ещё двум важным заключениям о виде этого распределения:
1) на плоском диске имеется центральное утолщение, показанное на рис. 18, б.
2) мы находимся не в центре диска.
Это второе утверждение может шокировать тех эгоцентриков, взгляды которых на наше положение во Вселенной сложились в эпоху после Коперника. Как отмечалось выше, Арьябхата утверждал, что не небесная сфера вращается вокруг Земли, а наоборот, Земля вращается по отношению к неподвижной небесной сфере. Из работ Николая Коперника (1473—1543 гг.) и астрономов более позднего времени, таких как Иоганн Кеплер (1571—1630 гг.), стало ясно, что Земля вращается не только вокруг своей полярной оси, но и вокруг Солнца по эллиптической орбите. Когда два астронома, отец и сын, Вильям Гершель (1738—1822 гг.) и Джон Гершель (1792—1871 гг.) обнаружили дискообразную структуру Млечного Пути, они посчитали, что наша Солнечная система находится в центре диска. Лишь в начале 20-х годов нашего века Харлоу Шепли (1885—1972 гг.) отодвинул Солнце из центра на периферию: как показано на рис. 19, Солнце находится примерно на двух третях расстояния от центра до края диска. На рис. 19 показано, на что похожа система звёзд, входящая в Млечный Путь, если посмотреть на неё снаружи. Заметим, что в этой системе имеются два закручивающихся наружу спиральных рукава. Эти рукава являются областями с наибольшей плотностью звёзд.
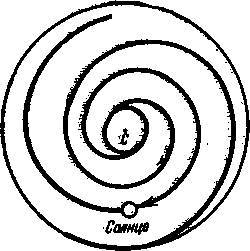
Рис. 19. На схематическом рисунке нашей Галактики видны два спиральных рукава
Чтобы представить всю картину в правильном масштабе, заметим, что полное число звёзд в распределении на рис. 18 и 19 оценивается в 200 миллиардов. Сам диск имеет диаметр порядка 100 000 световых лет и толщину порядка 10 000 световых лет. Принято называть всю эту грандиозную систему Галактикой. Кроме звёзд, в Галактике имеются также газ и пыль в рассеянной форме, но об этих составных частях Галактики мы поговорим позднее.
Что такое световой год? Свет летит со скоростью около 300 000 км/с. Световая секунда — это расстояние, покрываемое светом за 1 с, т. е. 300 000 км. Аналогично, световая минута равна расстоянию в 18 млн. км, световой час чуть больше 1 млрд. км, а световой год приблизительно равен 9,2 трлн. км! Таблица 4. Приближённые значения длительности путешествий
внутри Галактики со скоростью светаПутешествиеДлительность Земля — Солнце 8 мин Солнце — Сатурн 11/4 ч Солнце — Плутон (край Солнечной системы) 51/4 ч Солнце — Проксима Центавра (ближайшая звезда) 41/4 года Солнце — Крабовидная туманность (см. рис. 53) 6000 лет Солнце — центр Галактики 30 000 лет Центр Галактики — край Галактики 50 000 лет Полный периметр Галактики 300 000 лет
Эти цифры могут дать некоторое представление о гигантских размерах Галактики. В табл. 4 указано время, которое нужно затратить, чтобы осуществить воображаемое путешествие с Земли до разных астрономических объектов внутри Галактики (подразумевается, конечно, что мы можем двигаться без остановок со скоростью света). РАССТОЯНИЕ ДО СОЛНЦА
Попробуем теперь шаг за шагом искать ответ на вопрос: «Далеко ли до звёзд?» По существу, мы хотим объяснить, как были измерены расстояния, упомянутые выше. Начнём с ближайшей звезды — Солнца.
Часто используемый метод определения астрономических расстояний иллюстрируется примером; приведённым на рис. 21. Здесь показан маяк на острове, видимый с материка. Мы хотим определить расстояние до маяка, не покидая материк, что совершенно аналогично задаче астрономии.
Рис. 20. Иллюстрация к методу триангуляции
Как видно из рис. 20, задача решается методом триангуляции Пусть мы наблюдаем, маяк СД из двух опорных течек А и В на материке. Можно измерить расстояние АВ и углы САВ и СВА. Тогда не составляет труда нарисовать треугольник ABC на бумаге, выбрав подходящий масштаб для расстояния АВ. В результате мы узнаем, где находится С по отношению к A и B, т.е. узнаем расстояние от С до любой точки, на материке. Линия АВ называется базой этой триангуляции.
Рис. 21. Небольшая погрешность в измерении базовых углов А и В легко может изменить оценку расстояния до удалённого объекта, отодвинув его из точки С в точку С'
Поскольку астрономические объекты очень далеки, необходимо использовать очень большую базу. Если этого не сделать, наш треугольник АВС будет чересчур «тонким» в том смысле, что угол АСВ будет очень малым. Небольшая погрешность в измерении этого угла приведёт к большой погрешности в оценке расстояния до источника света. На рис. 21 проиллюстрирована опасность такой погрешности.
Понятно, что наибольшую базу на Земле можно получить, производя измерения на концах её диаметра. Эти точки отстоят друг от друга примерно на 12 800 км. Как ни велико это расстояние, все же оно недостаточно для того, чтобы аккуратно определить расстояние до Солнца. Но такую базу можно использовать для определения расстояния до Марса, когда он находится ближе всего к Земле. Такое случается, когда Солнце (С), Земля (3) и Марс (М) находятся на одной прямой с Землёй, посередине. Это расположение показано на рис. 22. В такой ситуации можно с помощью триангуляции измерить расстояние ЗМ.
Рис. 22. Диаграмма, иллюстрирующая метод измерения расстояний от Солнца (С) до Земли (3) и Марса (М)
Но как же измерить расстояние от Земли до Солнца (СЗ)? Для этого можно воспользоваться законами Кеплера движения планет. Третий закон Кеплера утверждает, что квадрат периода обращения планеты вокруг Солнца меняется пропорционально кубу расстояния планеты до Солнца. Марсианский период обращения равен 687 дней, а период обращения Земли — 365¼ дней. Поэтому из закона Кеплера получаем соотношение
(CM/СЗ)³ = (687/365¼)² .
Решая это уравнение, находим, что приблизительно СМ=(3/2) СЗ. Отсюда ЗМ=СЗ/2, и мы можем узнать СЗ, если перед этим узнали значение ЗМ.
Конечно, метод измерений описан нами несколько упрощённо. На самом деле планеты движутся по эллиптическим орбитам вокруг Солнца и математически задача определения СЗ более сложна, чем для круговых орбит на рис. 22. Однако наш пример правильно передаёт сам принцип измерения расстояния.
Благодаря современной технологии сейчас имеются лучшие способы измерения, чем старый метод триангуляции с использованием Марса. Посылая сигналы радиолокатора на планету Венера (В) в тот момент, когда она находится между Землёй и Солнцем, можно измерить непосредственно её расстояние до Земли. Действительно, сигнал радиолокатора — это одна из форм микроволнового излучения, которое (как было объяснено в гл. 2) распространяется со скоростью света. Следовательно, если сигнал, отправленный на Венеру, и его эхо, принятое на Земле, разделяет промежуток времени 300 с, можно заключить, что путь в один конец, равный расстоянию ЗВ, составит половину всего пути, пройденного светом за указанный промежуток времени.