Сама добротность Q определяется как f0/BW и равна RB/RF. При изменении значения центральной частоты (с помощью RF) пропорционально изменяется и добротность Q, при этом сохраняется неизменной ширина полосы пропускания Qf0.
Когда вы проектируете биквадратный фильтр вчерновую (правильнее использовать ИС активного фильтра, которая уже содержит большинство необходимых элементов), то основная методика определяется следующим образом:
1. Выберем ОУ с шириной полосы пропускания fс, которая по крайней мере в 10–20 раз превышает Qf0.
2. Подберем округленный номинал конденсатора, ближайший к следующему значению С = 10/f0 мкФ.
3. Используем требуемое значение центральной частоты для расчета значения сопротивления RF согласно приведенному выше первому уравнению.
4. Используем второе расчетное уравнение для вычисления по заданному значению ширины полосы пропускания номинала сопротивления RG.
5. Исходя из требуемого коэффициента передачи на центральной частоте полосы пропускания и согласно третьему расчетному уравнению получаем значение сопротивления RG.
Если расчетные значения сопротивлений получаются слишком велики или слишком малы, что неудобно в некоторых случаях, то можно подобрать другой номинал конденсатора. Например, в высокодобротном фильтре потребуется использовать увеличенное значение конденсатора С, отчасти с тем чтобы предотвратить существенное увеличение значение сопротивления RB (или можно использовать описанную в разд. 4.19 Т-образную цепь). Следует отметить, что каждое из сопротивлений RF, RB и RG является нагрузкой для ОУ и, следовательно, их значение не должно становиться меньше, скажем, 5 кОм. Манипулируя номиналами элементов схемы, можно найти их значения, так чтобы просто удовлетворялось требование 1 путем уменьшения коэффициента передачи интегратора (увеличение значения RF) при соответствующем увеличении коэффициента передачи инвертирующего каскада (увеличение значения резистора обратной связи, которое в исходной схеме составляет 10 кОм).
Для иллюстрации предположим, что желательно спроектировать фильтр с теми же характеристиками, как в последнем упражнении. Мы должны начать с того, что временно зададим С = 0,01 мкФ. Затем найдем RF= 15,9 кОм (f0 = 1 кГц) и RB = 796 кОм (Q = 50; BW = 20 Гц). Наконец, RG = 79,6 кОм (G = 10).
Упражнение 5.5. Необходимо спроектировать полосовой фильтр со следующими параметрами: f0 = 60 Гц, BW = 1 Гц и G = 100.
Полосовые фильтры высокого порядка. Как и для рассмотренных ранее фильтров нижних и верхних частот имеется возможность проектировать полосовые фильтры более высоких порядков с приблизительно плоской полосой пропускания и крутым переходом к полосе задерживания. Это можно сделать с помощью каскадного соединения нескольких полосовых фильтров более низкого порядка, комбинируя их таким образом, чтобы обеспечить характеристику фильтра требуемого вида (Баттерворта, Чебышева и любые другие). Как и раньше фильтр Баттерворта имеет «максимально плоскую» характеристику, в то время как фильтр Чебышева удовлетворяет требованиям плоской характеристики в полосе пропускания при крутых скатах (переходной области).
Только что рассмотренные полосовые схемы, такие как фильтры на ИНУН, биквадратные фильтры и фильтры на основе метода переменных состояния, являются фильтрами второго порядка (два полюса). Увеличение крутизны характеристики фильтра путем добавления дополнительных секций приводит, как правило, к ухудшению переходной и фазо-частотной характеристик. Сама «ширина полосы пропускания» полосового фильтра определяется как ширина характеристики между точками —3 дБ, кроме, естественно, равноволновых фильтров, для которых эта ширина определяется точками, где характеристика спадает на величину пульсации в полосе пропускания.
В справочниках по активным фильтрам или в технических руководствах по применению ИС активных фильтров приводятся таблицы и методики проектирования таких сложных фильтров. Существует также несколько прекрасных программ по расчету фильтров, которые предназначены для недорогих машин (IBM PC, Macintosh).
5.09. Двойной Т-образный фильтр-пробка
Изображенная на рис. 5.21 пассивная RC-цепь имеет бесконечное затухание на частоте, равной fc = 1/2πRC.
Рис. 5.21. Пассивный двойной T-образный фильтр-пробка.
Такое бесконечное ослабление для RС-фильтров, вообще говоря, не характерно — данный фильтр действует столь эффективно благодаря сложению двух сигналов, которые на частоте среза имеют разность фаз в 180°. Получение достаточно близкого к нулю значения характеристики на частоте fc требует хорошего согласования элементов. Этот фильтр называется двойным Т-образным и может употребляться для устранения сигнала помехи, например сетевой наводки 60 Гц. Трудность состоит в том, что характеристика этой цепи такая же «мягкая», как и у всех пассивных RC-цепей, и лишь в окрестности частоты fc обрывается почти отвесно. Например, двойная Т-образная цепь, управляемая идеальным источником напряжения, имеет затухание 10 дБ на частоте, равной удвоенной (или половинной) частоте fc, и ослабление 3 дБ на частоте, равной учетверенной (или деленной на четыре) частоте fc. Один из способов улучшить характеристику этой цепи — сделать ее «активной» — по типу фильтра Саллена и Ки (рис. 5.22).
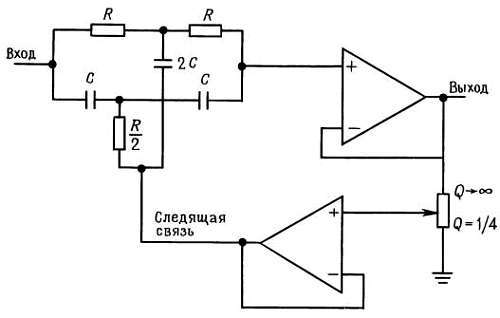
Рис. 5.22. Т-образный фильтр со следящей связью.
Эта идея кажется в принципе хорошей, но на практике разочаровывает из-за невозможности сохранения хорошего затухания на частоте нуля. Дело в том, что при увеличении резкости провала характеристики (большее усиление в петле следящей связи) ослабление на частоте нуля уменьшается.
Двойные Т-образные фильтры выпускаются в виде готовых модулей на диапазон частот от 1 Гц до 50 кГц с глубиной ослабления на частоте провала около 60 дБ (с некоторым ухудшением при высоких и низких температурах). Такие фильтры легко собрать из отдельных элементов, но для получения глубокого и стабильного провала следует выбирать конденсаторы и резисторы со стабильными параметрами и низкой температурной зависимостью. Один из элементов должен быть регулируемым.
Двойной Т-образный фильтр функционирует прекрасно при фиксированной частоте провала, но основные трудности возникают при попытке сделать его перестраиваемым, поскольку три резистора необходимо изменять одновременно, сохраняя постоянным их соотношение. Однако замечательная своей простотой изображенная на рис. 5.23, а RC-схема, которая ведет себя аналогично двойной Т-образной схеме, может перестраиваться в широком диапазоне частот (по крайней мере две октавы) с помощью единственного потенциометра.
Подобно двойному Т-образному фильтру (как и большинство активных фильтров), для него требуется провести определенное согласование элементов; в этом случае номиналы всех трех конденсаторов должны быть идентичны, а значение фиксированного резистора должно точно в шесть раз превышать значение нижнего (регулируемого) резистора. Сама частота подавления определяется следующим образом: