Насколько точно эти поля описывают слабое взаимодействие? Они призваны компенсировать изменение от точки к точке степени смешивания электронов и нейтрино. (Теория Вайнберга—Салама применима также к другим лептонам и кваркам.) Это означает, что при испускании или поглощении кванта поля, природа частицы тут же изменяется. Электрон может превратиться в нейтрино, нейтрино – в электрон. Именно так и происходит под действием слабых сил.

На рис. 17 показан типичный процесс, обусловленный слабым взаимодействием. Экспериментатор наблюдает его при столкновении (рассеянии) нейтрона (n) и нейтрино (нюе), когда обе частицы превращаются в протон (р) и электрон (е). При более детальном описании с использованием частиц-переносчиков d-кварк в нейтроне превращается в u-кварк (тем самым нейтрон превращается в протон) с испусканием виртуальной частицы (на диаграмме показана пунктиром), которая затем поглощается нейтрино (при этом нейтрино превращается в электрон). Так как протон обладает положительным электрическим зарядом, виртуальная частица должна уносить отрицательный заряд (по закону сохранения электрического заряда). Этот отрицательный заряд “оседает” на электроне. Отрицательно заряженный переносчик слабого взаимодействия получил название W–чacтицы. Должна существовать и положительно заряженная античастица W+, которая служила бы переносчиком слабого взаимодействия, например, от антинейтрона к антинейтрино.

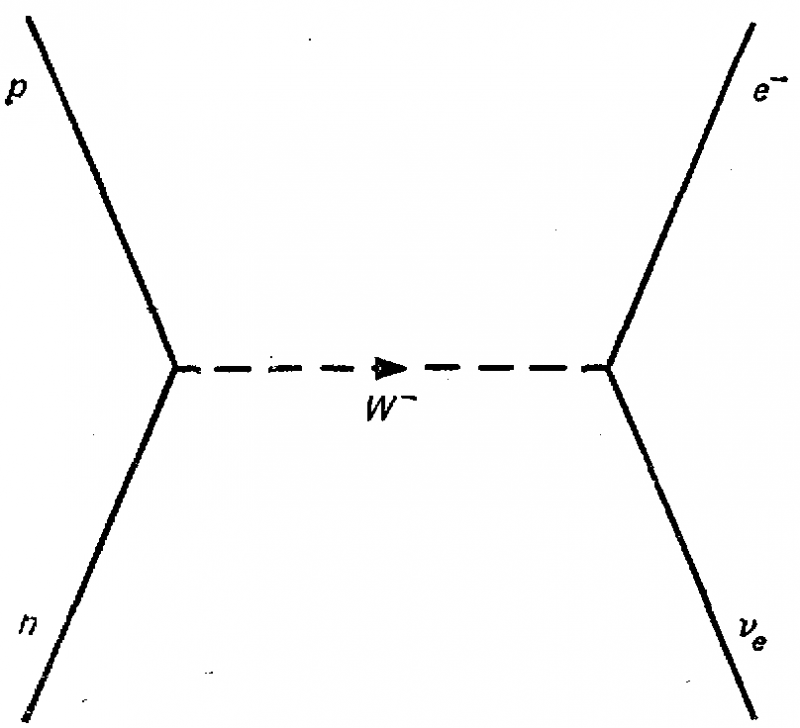
Рис.17. В процессе слабого взаимодействия, происходящего при столкновении нейтрона (n) с нейтрино (нюе), они превращаются в протон (р) и электрон (е-). Тщательный анализ показывает, что это превращение происходит в результате обмена тяжелой заряженной частицей (промежуточным векторным бозоном W-) Обмен W– соответствует превращению нейтрона в протон, причем в момент испускания изменяется аромат одного из образующих нейтрон кварков (d -> и)

Частицы W+ и W– являются переносчиками двух из трех связанных со слабым взаимодействием полей, предсказанных теорией Вайнберга – Салама. Третье поле соответствует электрически нейтральной частице-переносчику, получившей название Z-частицы. Когда теория Вайнберга – Салама была сформулирована впервые, мысль о нейтральной частице – переносчике слабого взаимодействия была новой. Существование Z-частицы означало бы, что слабое взаимодействие могло бы не сопровождаться переносом электрического заряда. Пример такого процесса приведен на рис. 18: электрон и нейтрино рассеиваются, обмениваясь Z-частицей. В 1973 г. в длительном эксперименте, проведенном в ЦЕРНе, было продемонстрировано существование нейтральных переносчиков слабого взаимодействия. Этот результат поднял престиж теории Вайнберга – Салама.

Несмотря на столь счастливое согласие между теорией и экспериментом, описанию слабого взаимодействия как калибровочного поля еще предстояло преодолеть серьезное препятствие. Дело в том, что калибровочные поля по своей природе дальнодействующие, казалось, что теория неизбежно должна предсказывать нулевую массу покоя частиц-переносчиков, как в случае фотона. В действительности же слабое взаимодействие существует лишь на очень малых расстояниях, и частицы – переносчики слабого взаимодействия имеют огромную массу. Если в теории W– и Z-частицам просто приписать какую-нибудь массу, то калибровочная инвариантность нарушится. Как наилучшим образом совместить несовместимое – калибровочную симметрию и частицы-переносчики с ненулевой массой покоя?

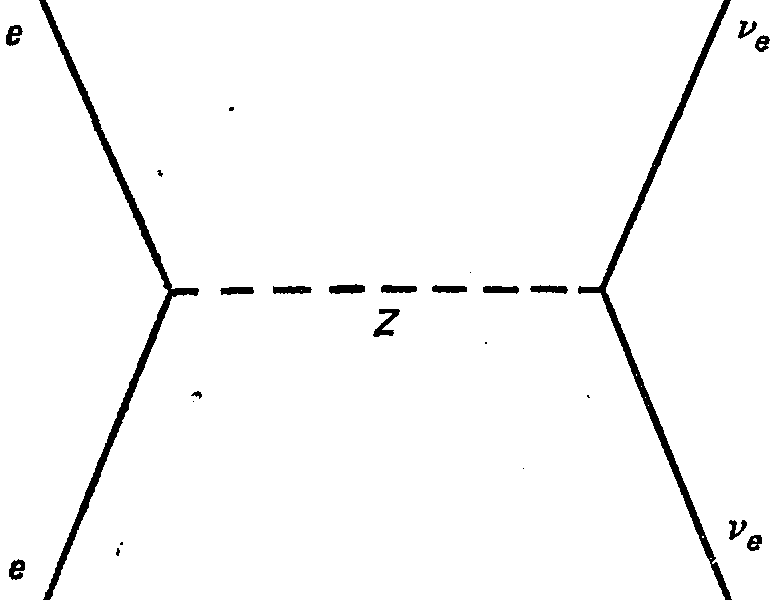
Рис.18. Теория Ваинберга—Салама предсказывает, что электроны могут рассеивать нейтрино, обмениваясь с ними электрически нейтральным переносчиком слабого взаимодействия – промежуточным векторным бозоном Z. Экспериментальное подтверждение такого процесса было получено в середине 70-х годов,

Решение этой головоломки было найдено Вайнбергом и Саламом в 1967 г. В основе его лежала остроумная идея, получившая название спонтанного нарушения симметрии. Вот как оно происходит.

Представим себе гладкую поверхность в форме мексиканского сомбреро, покоящегося на горизонтальном основании (рис. 19). Поместим на верхушку “сомбреро” шарик. В такой конфигурации система обладает очевидной симметрией, а именно: она не меняет своего вида при поворотах вокруг вертикальной оси, проходящей через центр шляпы. Если рассматривать только гравитацию, то никакого выделенного горизонтального направления здесь нет (гравитация действует по вертикали); все точки на полях сомбреро равнозначны.

Рассматриваемая система симметрична, но не устойчива. Стоит шарику тронуться с места, как он скатится вниз и остановится где-то на полях “сомбреро”. Как только это произойдет, симметрия системы нарушится. Шарик остановится в определенном месте на полях шляпы, задав тем самым выделенное горизонтальное направление от центральной оси. Устойчивость оплачена нарушением симметрии. В устойчивой конфигурации исходная вращательная симметрия сил (в нашем случае – гравитации) по-прежнему существует, по в скрытом виде. Наблюдаемое состояние системы не отражает симметрии тех взаимодействий, которые проявляются в системе.

Ту же общую идею использовали Вайнберг и Салам, хотя симметрия на этот раз была калибровочной, а не вращательной, и спонтанное нарушение соответствовало квантовому состоянию силовых полей. Таким образом, в теории Вайнберга и Салама поля по-прежнему обладают фундаментальной симметрией, по не могут нормально существовать в состоянии, обладающем этой симметрией, так как это состояние неустойчиво. Поэтому поле “выбирает” устойчивое состояние, в котором симметрия нарушена, а частицы – переносчики слабого взаимодействия обладают массой. Естественно, в деталях теория гораздо сложнее примера с “мексиканским сомбреро”, но основная идея все та же: симметрия по-прежнему присуща фундаментальным законам, но не проявляется в реальном состоянии системы. Именно поэтому физикам не удавалось обнаружить эту крайне важную калибровочную симметрию в течение тридцати пяти лет исследований слабого взаимодействия.

Чтобы получить решающее спонтанное нарушение симметрии, Вайнберг и Салам ввели в теорию дополнительное поле – так называемое поле Хиггса (в честь Питера Хиггса из Эдинбургского университета, который ранее изучал спонтанное нарушение симметрии в физике элементарных частиц). Никто никогда не видел поля Хиггса, но его наличие может оказывать решающее влияние на поведение калибровочных полей. В примере с сомбреро симметричное состояние – с шариком на самой верхушке шляпы – неустойчиво. Шарик “предпочитает” скатиться на поля, так как у состояния с нарушенной симметрией более низкая энергия. Аналогичным образом свойства поля Хиггса таковы, что состоянию с наименьшей энергией соответствует нарушение симметрии. Именно благодаря связи между полем Хиггса и калибровочными полями у W– и Z-частиц возникает масса. Теория Вайнберга – Салама предсказывает также существование частицы Хиггса – кванта поля Хиггса, или бозона Хиггса – с нулевым спином и большой массой.

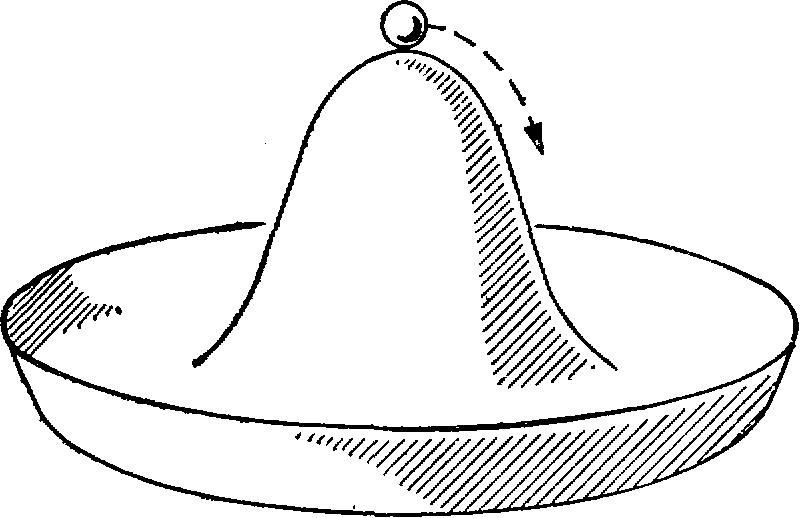
Рис.19. Спонтанное нарушение симметрии. Шарик помещен на вершину поверхности, имеющей форму мексиканского сомбреро. Такая система обладает полной вращательной симметрией, но она неустойчива, и шарик самопроизвольно скатывается на поля “сомбреро”, останавливаясь в произвольной точке. Вращательная симметрия при этом нарушается. Система обретает устойчивость ценой потери симметрии.

Воспользовавшись идеей спонтанного нарушения симметрии, Вайнберг и Садам сделали следующий важный шаг, соединив электромагнетизм и слабое взаимодействие в единой теории калибровочного поля. Чтобы единая теория включала поля обоих типов, необходимо было начать с более сложной калибровочной симметрии, которая сочетает в себе и более простую калибровочную симметрию электромагнитного взаимодействия и изотопическую симметрию слабого взаимодействия. Таким образом, в теории Вайнберга – Салама представлено всего четыре поля; электромагнитное поле и три поля, соответствующие слабым взаимодействиям. Следующий шаг состоял во введении поля Хиггса, которое могло бы вызвать спонтанное нарушение симметрии. Первоначально W– и Z-кванты не имеют массы, но нарушение симметрии приводит к тому, что некоторые частицы Хиггса сливаются с W– и Z-частицами, наделяя их массой. По образному выражению Салама, W– и Z-частнцы “поедают” частицы Хиггса, чтобы прибавить в весе. Фотоны не участвуют в этом процессе в остаются безмассовыми.