Теоретическое распределение коэффициента корреляции между независимыми переменными для трех точек в соответствии с формулой, выведенной Фишером (слева), и результат моделирования, выполненного 10 000 раз (справа).
Если даны четыре точки, то все значения коэффициента корреляции равновероятны. Если дано пять точек, то наиболее вероятным значением является ноль. По мере роста числа точек начинает вырисовываться традиционный график в форме колокола.
* * *
Еще один пример: сбалансированы ли игральные кости?
В главе 2 упоминается, что в 1850 году швейцарский астроном бросил пару игральных костей (красного и белого цвета) 20000 раз. Полученные результаты были достаточно далеки от ожидаемых теоретических значений. Это дает основания подозревать, что в эксперименте, возможно, использовались несбалансированные игральные кости. Так как все шесть возможных результатов являются равновероятными, если мы бросим игральные кости 20 000 раз, то теоретически каждое значение выпадет 20000/6 = 3333 раза. В следующей таблице представлены результаты эксперимента, теоретические значения и абсолютная величина отклонения от теоретических значений.
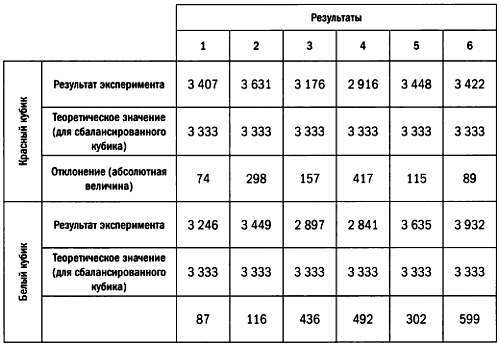
Являются ли эти отклонения достаточно большими, чтобы говорить о несбалансированности игральных костей? Или же эти отклонения могут возникнуть случайным образом? В конце концов, если бы результаты эксперимента в точности совпадали бы с теоретическими значениями, это тоже выглядело бы странно. Чтобы развеять сомнения, проверим статистическую гипотезу по той же схеме, что использовал Фишер для решения задачи о дегустаторе чая. Будем предполагать, что игральные кости сбалансированы, и отвергнем эту гипотезу только в том случае, если полученные данные будут явно ей противоречить.
Будем анализировать максимальное отклонение между полученными и теоретическими значениями. В предыдущей таблице показано, что для красного кубика эта величина равна 417, для белого — 599. Зададимся вопросом: каковы ожидаемые значения этой величины для идеально сбалансированных игральных костей? И снова на этот вопрос можно ответить с помощью моделирования.
Смоделируем 20000 бросков игральной кости, подсчитаем, сколько раз выпадет каждое значение, и рассчитаем максимальное отклонение от теоретического значения. При первом моделировании максимальное отклонение равнялось 83, при втором — 97. После того как моделирование было выполнено 10000 раз, была получена гистограмма, представленная на следующем рисунке. На ней также указаны значения, соответствующие красному и белому игральному кубику.
Распределение максимального отклонения для сбалансированных игральных костей и значения, полученные экспериментально.
Очевидно, что данные эксперимента противоречат гипотезе о сбалансированности игральных костей. Если бы эта гипотеза была верна, то вероятность получить подобные данные была бы очень, очень мала. В этом случае р-значение равно нулю с точностью до нескольких знаков после запятой. Следовательно, мы можем утверждать, что игральные кости несбалансированны, а вероятность того, что мы ошибаемся, практически равна нулю.
В качестве показателя, обобщающего данные эксперимента, можно использовать не максимальное отклонение, а величину, в которой учитывается отклонение для всех шести возможных результатов броска игральной кости.
Такой величиной может быть сумма всех отклонений, равных разности фактической и теоретической частоты, возведенных в квадрат (чтобы положительные и отрицательные отклонения не скомпенсировали друг друга), разделенная на теоретическую частоту.
Для красной игральной кости эта величина будет равна
Расчеты могут показаться вам излишне сложными, но эта величина обладает определенным преимуществом: она не требует моделирования распределения для случая, когда нулевая гипотеза верна (так называемого эталонного распределения). Эта величина называется критерий х2 (хи-квадрат). Ее впервые использовал в 1900 году Карл Пирсон, сыгравший важную роль в истории статистики. Мы уже упоминали его имя, когда говорили о коэффициенте корреляции.
Для обычных статистических тестов нет необходимости в моделировании распределения величины. Вместо этого оно выводится с помощью математических методов. Формула для расчета распределения коэффициента корреляции достаточно сложна и не имеет своего названия, хотя при большом размере выборки это распределение близко к нормальному. Первым, кто вывел формулу для этого распределения, был не кто иной, как Рональд Эйлмер Фишер.
* * *
СЛИШКОМ МАЛОЕ ОТКЛОНЕНИЕ ТОЖЕ ПОДОЗРИТЕЛЬНО
Если мы бросим идеально сбалансированную игральную кость 20000 раз, то каждое из возможных значений выпадет примерно 20 000/6 = 3333 раза. Отклонение фактической и теоретической частоты редко превышает 250. Это происходит всего один раз на каждые 100000 симуляций.
Однако также весьма необычно, если фактические значения очень близки к теоретическим. Допустим, игральная кость была брошена 20000 раз и были получены следующие результаты:

Есть основания подозревать, что эта информация недостоверна, так как столь малое отклонение фактической и теоретической частоты встречается всего один раз на миллион.
Фишер обнаружил любопытное совпадение между экспериментальными данными, опубликованными Менделем в его знаменитых работах о наследственности, и ожидаемыми теоретическими значениями. Удивительнее всего то, что Мендель ошибочно спрогнозировал результаты некоторых экспериментов, но полученные данные тем не менее были подозрительно близки к прогнозным значениям. По мнению Фишера, данные скорректировал необязательно сам Мендель, а кто-то из его ассистентов, который недобросовестно отнесся к работе и решил подменить реальные данные именно теми, которые ожидал увидеть Мендель.
Этот вопрос спровоцировал бурное обсуждение. Эта задача относится не только к теории вероятности, но также к генетике и ботанике, так как в ней идет речь о фундаментальном механизме наследования признаков у растений. Споры не утихали длительное время, но какой-то определенный итог этих дискуссий подвести трудно. Стороны сходятся на том, что нет четких доказательств того, что Мендель или кто-то еще скорректировал результаты эксперимента.
* * *
До сих пор это верно, далее — нет: границы р-значения
Как правило, выбирается определенное p-значение, чаще всего 5 %, и если полученное на практике p-значение оказалось меньше, то нулевая гипотеза отвергается, в противном случае — нет. Это значение называется уровнем значимости.
Конечно, всем нам нравятся четкие и простые правила, но было бы неразумно выбрать одно универсальное значение и применять его всегда вне зависимости от контекста. Выбор граничного значения равносилен выбору вероятности того, что мы ошибочно отвергнем нулевую гипотезу. Вероятность ошибки, которую будет разумно выбрать, зависит от ситуации и возможных последствий ошибки.
Предположим, как-то утром, выходя из дома, мы смотрим прогноз погоды и решаем, что вероятность дождя равна 10 %. Стоит ли взять с собой зонтик? Если мы не возьмем с собой зонтик и примем 10-процентный риск попасть под дождь, никому из нас это не покажется неразумным. Если мы ошибемся, то потеряем немного (разве что слегка намокнем). Также следует учесть, что ходить весь день с зонтиком достаточно неудобно.