N = х₁·2⁰ + х₂·2¹ + х₃·2³ +…

Для передачи любого числа от 0 до 31 необходимо пять двоичных разрядов, или 5 бит информации. Таким образом, сообщение гангстера Лучано мафиози содержало 5 бит информации.

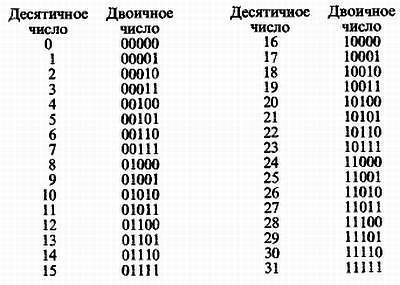
В народном хозяйстве необходимо передавать значительно больше информации. Не вызовет удивления, например, такая телеграмма, переданная работником снабжения: «В феврале на Чукотку поступило 10 000 грампластинок». Информация здесь такова: во-первых, февраль. Надо думать, поставки товаров подобного рода производятся ежемесячно, поэтому февраль надо обозначить цифрой 2. Отсюда определяем число двоичных разрядов, необходимых для передачи номера месяца: 4 (2⁴ = 16, имеется некоторая избыточность информации). Далее необходимо ввести код Чукотки. Пусть соответствующая организация поставляет товары в 120 краев и областей, причем Чукотке ввиду ее удаленности присвоен последний номер. Тогда для передачи кода Чукотки (120) потребуется 7 двоичных разрядов (2⁷ = 128). После кода области надо указать код товара. Если всего поставляется, например, 512 наименований товаров, то для обозначения грампластинок, скажем № 384, потребуется 9 разрядов (2⁹ = 512). И наконец, число грампластинок 10000 в двоичном коде займет 14 разрядов. Получаем следующую таблицу:

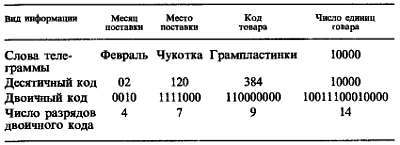
Полное сообщение требует 34 двоичных разряда. Спереди обычно добавляют несколько разрядов служебной информации адрес, знак начала сообщения и т. д. Последовательность кодов и число разрядов каждого кода, указанные в таблице, должны быть и у отправителя, и у получателя сообщения, чтобы они имели возможность закодировать и раскодировать телеграмму. На линии связи эти процессы автоматизированы, соответствующие устройства называют кодерами и декодерами.

В книгах про разведчиков подобные таблицы называются шифрами и ключами к шифрам, скажет сообразительный читатель, и будет совершенно прав. Надеюсь, что наиболее юные и энергичные из читателей придумывают свои собственные шифровальные таблицы для игры в разведчиков, и их шифры, особенно представленные в двоичном коде, вряд ли расшифрует «неприятель». Итак, мы научились представлять информацию в цифровой форме и определять ее объем. А как быть с аналоговыми сигналами? Раньше их обрабатывали в аналоговой форме, теперь все чаще преобразуют в цифровую.

Вспомним автопилот самолета, который мы уже рассматривали, и попробуем сконструировать простейший датчик углового положения фюзеляжа. Возьмем отвес — жесткий стержень с грузом на конце, закрепленный на горизонтальной оси 0. Верхний конец стержня соединим с подвижным контактом потенциометра R, а к крайним выводам потенциометра подключим источники напряжения -10 и + 10 В. Если фюзеляж самолета находится в горизонтальном положении, подвижный контакт будет в середине резистивной подковки потенциометра, а потенциал на нем U обратится в нуль.

Стоит самолету наклониться вперед, скажем войти в пике, движок потенциометра переместится влево по подковке и потенциал U станет отрицательным. Если же носовая часть самолета будет направлена вверх, потенциал U станет положительным. Пусть при наклоне фюзеляжа на угол ± 20° потенциал U изменяется от + 10 до —10 В. Крутизна характеристики преобразования угол напряжение для такого датчика составит 0,5 В на градус. Таким образом мы получим аналоговый сигнал углового положения самолета. Для преобразования этого сигнала в цифровую форму необходимо задаться шагом дискретизации — минимальным изменением напряжения, соответствующим изменению цифрового кода на единицу.

Если в нашем простейшем случае достаточна точность 1°, то шаг дискретизации будет равен 0,5 В. Число шагов дискретизации, на которое изменилось напряжение U, и будет являться углом наклона фюзеляжа, выраженным в градусах. Его значение можно представить и двоичным кодом, как это показано на рисунке.

Датчик углового положения.

Дискретизация по уровню.

Для преобразования аналоговых величии в цифровой код служат специальные электронные устройства — аналого-цифровые преобразователи (АЦП). Полученный цифровой код углового положения фюзеляжа поступает в цифровой процессор, выполняющий функции и сравнивающего устройства, и системы регулирования (посмотрите схему на стр. 19). Сюда же поступают сведения и о положении самолета в других плоскостях пространства, и о положении рулей. Процессор вырабатывает сигнал, управляющий рулями. При цифровой обработке информации можно получить значительно большую точность регулирования и управления. Этим и объясняется широкое применение цифровой техники в системах управления.

С какой точностью, например, можно измерить напряжение с помощью обычного стрелочного прибора? Лучшие лабораторные магнитоэлектрические приборы с зеркальной шкалой обеспечивают точность отсчета не более 0,2 %, что составляет 2·10^-3. В то же время цифровые вольтметры могут иметь пять-шесть разрядов, что обеспечивает точность измерений на два-три порядка (в 100… 1000 раз) выше. Но вернемся к проблемам связи, ведь мы так и не закончили разговор о передаче телефонных сигналов цифровым кодом.

Несколько лет назад мне довелось пройти на гидрографическом судне от Владивостока до Петропавловска-Камчатского. Естественно, что из каждого порта я звонил домой, в Москву, чтобы справиться о делах и здоровье близких. Владивосток был еще связан с Москвой старой системой аналоговой телефонной связи. Часа три приходилось ждать, пока телефонистки соединят линию. Наконец, еле-еле, сквозь шумы и трески послышался голос жены. Совсем иная картина была в Петропавловске. Там действовала цифровая телефонная связь. Прямо из кабины телефона-автомата можно набрать код Москвы, затем две-три служебные цифры и нужный номер в Москве. Весь процесс занял не более минуты, причем более половины этого времени ушло на то, чтобы разобраться в правилах пользования автоматом, вывешенных в кабине: какие набирать цифры, каких ждать гудков и т. д. Слышно было лучше, чем когда я звонил соседу по дому в Москве, так же хорошо слышали и меня, а помех практически не было. Надо ли говорить, что после состоявшегося разговора я стал ярым приверженцем цифровой телефонной связи.

Так как же обычная человеческая речь превращается в поток цифр, ведь на выводах микрофона имеется быстро изменяющийся речевой сигнал (как показано на рисунке)? А вот как. Берутся отсчеты, т. е. значения этого сигнала через равные промежутки времени τ. Интервал τ должен быть настолько мал, чтобы речевой сигнал не успевал намного измениться между отсчетами. Этот интервал часто называют временным шагом дискретизации или интервалом Найквиста. Минимальную частоту взятия отсчетов, т. е. величину, обратную временному шагу дискретизации, определяет теорема В. А. Котельникова (академика, основателя теории помехоустойчивости систем связи). Частота отсчетов должна быть вдвое больше самой высокой частоты звукового спектра. В телефонии принято передавать частоты только до 3400 колебаний в секунду, т. е. до 3,4 кГц. При этом разборчивость речи еще очень хорошая. Значит, частота взятия отсчетов должна быть не менее 6800 в секунду, или 6,8 кГц. Процесс взятия отсчетов называют дискретизацией по времени.