Поясним примером и графиком. Пусть вектор А^― вращается вокруг начала координат, угол поворота обозначим Ф. Тогда проекция вектора А^― на вертикальную ось будет у = A·sin Ф. Если еще учесть, что при равномерном вращении угол Ф нарастает прямо пропорционально времени: Ф = ω·t, где ω — угловая скорость вращения, то получится широко известная формула

у = A·sin ωt,

описывающая простое, синусоидальное колебательное движение. Точно такой же формулой описывается и переменное электрическое напряжение, имеющееся, например, в электрической розетке.

Синусоида — проекция равномерно вращающейся точки.

Мне кажется, теперь вы легко сможете ответить на вопрос, почему переменное напряжение в электросети синусоидально. Ведь якорь генератора на электростанции вращается равномерно. А магнитное поле, нужное для генерирования тока, направлено перпендикулярно оси якоря. Оно задает ту самую ось, на которую проектируется вращение якоря. Впрочем, гораздо лучше устройство генератора описано в школьном учебнике физики. Итак, в нашей электрической розетке имеется напряжение

u = A·sin ωt.

Названия параметров, входящих в формулу, стали несколько другими: А — амплитуда напряжения, ω — угловая частота, t — это по-прежнему текущее время. Если известно, что сетевое напряжение 220 В, это не значит, что А = 220 В. В электротехнике, если нет специальной оговорки, пользуются действующими значениями напряжения или тока. Действующие значения соответствуют значениям постоянного тока, развивающего ту же мощность. Амплитудное значение напряжения или тока в √2 раз больше действующего. Поэтому при действующем напряжении в сети 220 В мгновенное напряжение изменяется от нуля до 311 В по закону синуса и А = 311 В.

Давайте обсудим, почему синусоидальная форма напряжения или тока является простейшей, в некотором смысле наилучшей формой. Как мы уже установили такую форму тока дает равномерно вращающийся якорь генератора. Но если какими-либо техническими ухищрениями сделать форму тока другой, например прямоугольной? Даст ли это какие-нибудь преимущества при передаче электроэнергии? Оказывается, нет!

Синусоидальные колебания.

Прямоугольную волну тока можно представить как сумму простейших синусоидальных волн. На рисунке показано, как это делается. Сверху изображено синусоидальное колебание с частотой f₀. Напомним, что угловая частота связана с обычной, циклической частотой простым соотношением ω = 2π·f. Частота тока электрических сетей в СССР выбрана равной 50 Гц, в США 60 Гц. Это соответствует частоте вращения якоря генератора 3000 и 3600 об/мин соответственно. Если к изображенному на рисунке основному колебанию с частотой f₀ добавить еще одно колебание с частотой 3f₀ (третью гармонику основного колебания), то форма суммарного колебания изменится. Добавим еще и пятую гармонику-колебание с частотой 5f₀. Относительные амплитуды гармоник должны уменьшаться обратно пропорционально частоте. Результат суммирования трех колебаний с частотами f₀, 3f₀ и 5f₀ и с амплитудами 1, 1/3 и 1/5 изображен на нижнем графике. Здесь мы видим поразительное приближение к прямоугольному колебанию.

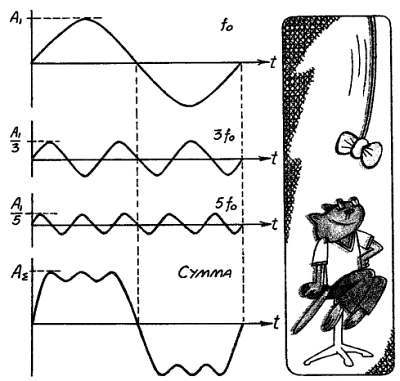
Прямоугольное колебание можно представить суммой синусоидальных гармоник с амплитудами А_n = A₁/n (где n = 1, 3, 5…)

Великий французский математик Ж. Фурье доказал, что любое периодическое колебание можно представить суммой простейших, синусоидальных колебаний с кратными частотами. Их набор называется спектром исходного колебания. Спектр можно изобразить графически, отложив по горизонтали частоты, а по вертикали относительные амплитуды гармоник. Точное приближение к исходной форме колебания дает чаще всего лишь бесконечный ряд гармоник. Например, для точного воссоздания симметричного прямоугольного колебания нужен бесконечный ряд нечетных гармоник основной частоты. Разумеется, передать такой сложный спектр по проводам электрической сети намного труднее, чем одну-единственную спектральную гармонику синусоидального колебания. Высшие гармоники неизбежно будут ослабляться по амплитуде, да и фаза их изменится, что приведет к искажению передаваемого прямоугольного колебания. Только синусоидальное колебание меньше всего подвержено искажениям при передаче.

Чем реже происходят колебания, тем больше их период (т. е. время совершения одного полного колебания) и тем ниже основная частота спектра этих колебаний. Спектральные линии на оси частот при этом располагаются гуще. Непериодический процесс тоже можно представить спектром, но спектр окажется уже не состоящим из отдельных спектральных линий, а сплошным. Соответствующая математическая операция называется интегральным преобразованием Фурье. Оно используется главным образом для импульсных сигналов. Характерна следующая закономерность: чем короче импульс, тем шире его спектр. Наивысшая частота спектра приблизительно обратно пропорциональна длительности импульса. Например, импульс длительностью 0,01 с имеет ширину спектра около 100 Гц, а импульс длительностью 1 мкс (10^-6) — 1 МГц. Особый интерес представляют бесконечно короткие или, как их еще называют, дельта-импульсы (δ-импульсы). Оли обладают бесконечно протяженным равномерным спектром (см. рисунок).

Звук падения одной капли дождя — это слабый и очень короткий щелчок. Он содержит колебания всех возможных звуковых частот — от самых низких до самых высоких. Шум дождя вы, разумеется, слышали и прекрасно себе представляете. Он складывается из отдельных звуков падения множества капель. Спектр шума дождя равномерен — его интенсивность одинакова на всех звуковых частотах. В электронике есть отличный аналог шума дождя — дробовой шум радиоламп и полупроводниковых приборов. Пролет каждого элементарного носителя электрического заряда, электрона или иона, создает в цени короткий импульс тока. А сумма множества таких импульсов образует электрический дробовой шум, очень похожий на шум дождя, если его воспроизвести через громкоговоритель. Собственно, само название «дробовой шум» произошло от звука дроби, ссыпаемой в какой-либо сосуд.

Прямоугольное колебание и его спектр.

Не напомнило ли вам что-нибудь это очень знакомое слово «спектр»? Спектр солнечного света, спектр радуги, спектр, полученный на экране с помощью стеклянной призмы… Что здесь общего со спектром электрических колебаний? Очень много. Разложение колебаний в спектр есть разложение на элементарные, синусоидальные колебания. Свет — это электромагнитная волна, распространяющееся электромагнитное колебание. А белый свет — это сумма бесконечного множества колебаний с различными частотами. Вот почему радисты называют шум с равномерным спектром белым.

Частоты световых колебаний можно найти, воспользовавшись связью между частотой и длиной волны: f = с/λ, где с — скорость света в вакууме, равная 3-10⁸ м/с, или 300000 км/с. Известно, что человеческий глаз реагирует на электромагнитные волны с длинами от 0,7 мкм (красный свет) до 0,4 мкм (синий свет). Частоты границ видимого диапазона составляют соответственно 4·10¹⁴ и 7,5·10¹⁴ Гц, т. е. 400 000 и 750 000 ГГц. Обратите внимание, насколько это больше частоты тока в электрической сети (50 Гц)! Оптики ввели понятие «монохроматическое колебание». Моно — значит единственный, хромос — цвет. Монохроматическое колебание имеет только одну, строго определенную частоту. Монохроматическая волна оптического диапазона воспринимается как густой, насыщенный цвет. Если вы когда-нибудь видели свет гелиево-неонового лазера (тонкий красный луч), обратили ли вы внимание на полную насыщенность цвета? Длина волны Не-Nе-лазера составляет 0,63 мкм, и его свет воспринимается как красный или красно-оранжевый. Других длин волн в излучении этого лазера нет. Если же электромагнитная волна имеет другую длину, она и воспринимается человеческим глазом как излучение другого цвета. Зеленый цвет соответствует длинам волн около 0,5 мкм, синий — 0,4 мкм.