Попытаемся понять физику эффекта, имея в виду кристалл А, на поверхности которого расположено некоторое поверхностно-активное вещество В. Может оказаться (и это оказывается в огромном количестве комбинаций А и В), что атомам сорта В выгодно расположиться между атомами сорта A, вклиниться между ними. Этому процессу можно помочь, приложив растягивающие усилия к кристаллу, и таким образом ослабить связь А—А. Если внедрение атомов сорта В в кристалл А произошло, в нем появляются связи типа А—В. А вот связи А—В могут оказаться значительно слабее связей А—А , и это может определить пониженную прочность кристалла.
К рассказанному необходимо добавить следующее. Основные события, сопутствующие разрушению, как правило, происходят в устье развивающейся трещины, к которой из слоя покрытия должны успевать приходить атомы сорта В. Их может поставлять либо процесс диффузии вдоль поверхности, либо процесс растекания вещества В по поверхности трещины, развивающейся в кристалле А.
При любом механизме эти поставки должны происходить достаточно быстро для того, чтобы у устья трещины были атомы сорта В, стремящиеся внедриться в кристалл Л. Здесь уместно обратить внимание на то, что эффекту Ребиндера свойственны многие черты и эффекта Иоффе, и эффекта Гриффитса. Их роднят особенности процесса развития трещины под действием напряжений.
А вот еще один опыт, иллюстрирующий иное проявление эффекта Ребиндера. В высокий стеклянный стакан наливается немного расплавленного галлия и на его дно ставится тонкая поликристаллическая пластинка цинка. Затем стакан заполняют специальным раствором, который очищает поверхность цинка. Далее происходит следующее. Галлий начинает ползти по поверхности цинка. Это видно отчетливо, так как на цинке образуется движущийся матовый след. Цинковая пластинка, покрытая галлием, начинает оседать на дно стакана, складываясь в гармошку или скручиваясь в рулон. Самопроизвольно, лишь под действием собственного веса!
Галлий, проникая в границы между зернами цинковой поликристаллической пластинки, ослабляет их, и зерна получают возможность легко взаимно смещаться. Именно это мы и видим, наблюдая, как мягко пластинка цинка оседает в стакане с галлием.
В первом опыте — аномальная хрупкость, во втором—аномальная пластичность. Можно было бы привести примеры резкого понижения твердости кристаллов горных пород и металлов, приобретения ими способности легко превращаться в порошок и много иных примеров изменения механических свойств кристаллических тел под влиянием поверхностно-активных веществ.
Читатель, даже не очень склонный к фантазированию, легко представит себе ту огромную роль, которую играет эффект Ребиндера в природе и во многих технологических процессах. Помогу читателю: в присутствии поверхностно-активных веществ легче обрабатывать резцом, легче штамповать, легче бурить горные породы, легче истирать кристалл в порошок...
«МОЗАИЧНЫЙ» КРИСТАЛЛ
Цель этого очерка — рассказать о том, как в реальном кристалле «поселился» дефект в виде границы между отдельными блоками, образующими кристалл. Рассказ следует начать издалека, с 1913—1914 гг., когда во многих лабораториях мира и теоретики и экспериментаторы, вдохновленные недавно сделанным открытием возможности исследовать структуру кристалла с помощью рентгеновских лучей, занимались изучением интенсивности лучей, отраженных от кристалла.
На первых порах в этих исследованиях при сопоставлении теории и эксперимента возникла сложная ситуация. Теоретики (как и подобает теоретикам!) построили теорию, основанную на предположениях, очень упрощающих задачу. Слово «очень» подчеркивается, так как теоретики предположили, что те вторичные волны, которые под влиянием падающего рентгеновского луча испускают атомы, ни между собой, ни с первичным лучом не взаимодействуют. В действительности, разумеется, взаимодействуют, и существенно, а теоретики этим пренебрегли. Вдумаемся: по существу, при этом они пренебрегли тем, что в кристалле атомы расположены упорядоченно, так как именно в связи с упорядоченностью взаимодействие между вторичными волнами может быть значительным. Практически вместо кристалла они рассмотрели просто совокупность независимых атомов. Изучая кристалл, они пренебрегли кристаллом! Назовем эту теорию «теория № 1».
После этой была построена более точная теория, учитывающая то, чем «теория № 1» пренебрегла. Назовем ее «теория № 2». Естественно ожидать, что «№ 2» — теория более точная — будет лучше согласовываться с результатами опытов, чем «теория № 1». А на поверку оказалось, что формулы «теории № 1» несравненно лучше описывают результаты измерений, чем формулы «теории № 2». Вот конкретный пример того, что скрывается за словом «лучше». Из опыта следует, что отражающая способность кристалла алюминия при одной из его ориентаций характеризуется числом 580. Из «теории № 1» следует число 818, а из «теории № 2» — 19,6.
Где же искать выход из этой странной ситуации, когда оказывается, что чем хуже, тем лучше? Ведь такой выход обязан быть! Вскоре он нашелся. Экспериментаторы заметили, что результаты измерений обычно оказываются между результатами, предсказанными каждой из теорий. Если кристалл немного исказить — продеформировать, пошлифовать поверхность, — результаты опытов приближаются к предсказаниям «теории № 1». Предсказания «теории № 2» эксперимент подтверждает лишь в редких, исключительных случаях, если опыт ставится с кристально чистым кристаллом, практически свободным от дефектов. Это свидетельство эксперимента указало путь к решению проблемы: теоретики предсказали, что модель идеального кристалла, лежащая в основе «теории
№ 2», — фикция. Реальный кристалл, видимо, состоит из маленьких областей-блоков. Блоки немного повернуты друг относительно друга и, следовательно, разделены границами. Вторичные волны, испускаемые взаимно повернутыми блоками, друг с другом практически не взаимодействуют, они «не в фазе». И поэтому, чем меньше размер блоков, тем в большей степени, с точки зрения первичного рентгеновского луча, реальный кристалл лишен строгой пространственной периодичности. А именно это молчаливо и предполагала несовершенная «теория № 1». Для согласования теории с экспериментом в то, теперь уже далекое, время физики оказались перед необходимостью умозрительно «поселить» в кристалле невидимый ими дефект — границу раздела между блоками, за которыми укрепилось название «блоки мозаики».
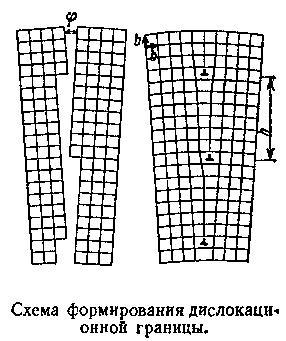
Многие годы «блоки мозаики» существовали не-увиденные, заявляющие о себе главным образом в опытах, в которых изучалась интенсивность рентгеновских лучей, отраженных поверхностью реального кристалла. Со временем, этак через четверть века, выяснилось, что границы между блоками представляют собой организованные ряды дислокаций. Структура этих границ зависит от того, из каких дислокаций они составлены и на какой угол друг относительно друга повернуты блоки, разделяемые границей.
В качестве примера границы между блоками мозаики обсудим простейшую границу, которая состоит из краевых дислокаций с одинаково ориентированными векторами Бюргерса. Воспользовавшись схемой такой границы, легко убедиться в том, что вектор Бюргерса b, расстояние между дислокациями h и угол между граничными блоками φ связаны соотношением
φ ≈ b / h
Если φ рад, то h ≈ b/φ ≈ 2• 10-4 см. При таком расстоянии между дислокациями они могут быть обнаружены обычной техникой химического травления!