Недавно в нашей лаборатории совершенно неожиданно студент-дипломник наблюдал капли, скачущие по твердой поверхности, когда ставил эксперименты по взрыву металлических проволочек, вплавленных в кристалл каменной соли.
Эксперимент заключался в следующем. Через проволочку импульсно пропускался электрический ток большой силы, и она взрывалась. Затем с помощью микроскопа исследовалась структура области кристалла вблизи взорвавшейся проволочки. При некоторых условиях осуществления взрыва кристалл растрескивался, и на оголившихся поверхностях можно было наблюдать пунктирные линии, состоявшие из пятнышек, которые оставила скачущая капля расплавленного металла проволоки.
Пунктирная последовательность следов во всех случаях завершалась каплей, которая, израсходовав свою энергию в скачках, прилипла к поверхности и закристаллизовалась на ней.
По фотографиям можно проследить некоторые особенности скачкообразного движения капли на поверхности кристалла. Но прежде чем это сделать — немного теории.
Допустим, что жидкая капля, радиус которой R , падает на плоскую поверхность под малым углом φ между поверхностью и направлением скорости. Если бы капля обладала свойствами абсолютно упругого тела, т. е. без потерь энергии отражалась от поверхности кристалла по закону «угол падения равен углу отражения» и воздух не препятствовал ее полету, она скакала бы по его поверхности сколь угодно долго и длина скачка l оставалась бы неизменной. Эту длину легко вычислить. Воспользуемся обозначениями, которые указаны на рисунке. Очевидно, в направлении, параллельном поверхности кристалла, капля, имея скорость υ 1 = υ 0 cosφ , будет лететь в течение всего того времени, которое понадобится ей для того, чтобы в поле земного тяготения вначале подняться от поверхности на максимальную высоту, а затем с этой высоты спуститься на поверхность кристалла. Это время -
τ = 2 υ 1 / g
В приведенных формулах мы воспользовались тем, что φ мало. Только в этом случае можно считать, что cos φ ≈ 1 , a sin φ ≈ φ .
Так было бы, если бы выполнялись обусловленные идеальные обстоятельства. В действительности капля, прыгая по твердой поверхности, теряет энергию. Во-первых, полету препятствует воздух и часть энергии расходуется на преодоление его сопротивления. Во-вторых, в момент удара капля вязко деформируется, а затем, оттолкнувшись от поверхности, восстанавливает свою форму. И на это необходима энергия. В-третьих, в каждой точке, где капля коснулась твердой поверхности, остается жидкое пятнышко. Его появление можно представить себе как отщепление от капли жидкой пластинки, т. е. появление двух свободных поверхностей жидкости, площадь каждой из которых равна площади оставленного пятнышка. При этом расходуется энергия Ws = 2а• S , где S — площадь пятнышка. Точно учесть все потери энергии скачущей капли — дело совсем не простое, так как они зависят от очень многого: скорости полета, массы капли, вязкости и поверхностного натяжения вещества капли. Величина этих потерь изменяется от скачка к скачку. Если сделать заведомо упрощающее предположение, что в каждом очередном скачке капля теряет одну и ту же энергию W , изменяя при этом массу незначительно, можно определить длину n-го скачка (l п) с помощью формулы, которая следует из предыдущей:
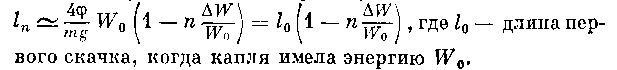
Полученная формула свидетельствует о том, что каждый следующий скачок должен быть короче предыдущего. Кроме того, из нее следует, что общее число скачков не может быть больше, чем п* = W 0 / Δ W . Фотографии подтвержда ют сделанные выводы: последующий скачок действительно короче предыдущего, и число скачков ограничено.
Так как конец пути капли на фотографиях запечатлен достовернее начала, можно надежно выяснить судьбу капли, прослеживая ее траекторию в направлении, противоположном направлению полета. Оказывается, что перед самым финишем на последнем этапе капля (которая изображена на приведенной фотографии) весила всего 4 . 10-8 г и имела энергию ~3 . 10- 6 эрг, т. е. ее скорость была немногим больше 10 см/сек.
Жидкая металлическая капля скачет по поверхности кристалла соли
А на предпоследнем этапе, с учетом того, что его длина и масса капли были большими, скорость полета капли оказывается существенно большей — около 100 см/сек. Двигаясь так от конца пути к его началу, можно восстановить все характеристики скачкообразного движения капли и вычислить, сколько и на что она тратила свою энергию при каждом очередном столкновении с поверхностью. Здесь мы этого делать не будем. Это сделал студент в своей дипломной работе.
Каплеподшипники
Иные идеи привлекают не столько практическими последствиями, сколько неожиданностью поворота мысли, талантливой курьезностью. Эстетическое наслаждение доставляет неожиданный взгляд на известное явление или процесс, решение, которое, казалось бы, на виду у всех, а заметил его кто-то один — более зоркий, менее предубежденный.
Идея каплеподшипников была высказана Я. И. Френкелем в 1950 году. В «Журнале технической физики» появилась короткая, в одну страничку, заметка, в которой излагалась идея и высказывалась надежда на то, что она, эта идея, быть может, окажется полезной приборостроителям. Существо идеи заключается в возможности замены в шарикоподшипниках стальных шариков жидкими каплями. Капли не смачивают поверхность гнезда и благодаря этому сохраняют свою индивидуальность. Правда, неожиданно? Каленую сталь предлагается заменить жидкостью!
Осуществить такую замену, пусть в небольших и не очень нагруженных подшипниках, заманчиво, так как технология изготовления стальных шариков, диаметр которых должен выдерживаться с большой точностью, очень сложна и дорога.
Идея возникла после того, как были подробно и тщательно изучены закономерности движения свободной капли по наклонной плоскости и капли, расплющенной между двумя пластинками, из которых одна покоится, а другая — движется. Имеется в виду, что вещество капли плохо смачивает или не смачивает твердую поверхность.
Чтобы капля двигалась, ей совсем не нужно быть сферической. Капля жидкая, и потому она может перемещаться вследствие переливания жидкости сзади (и сверху) вперед (и вниз). Такое движение — оно отлично наблюдается, когда дождевая капля ползет вниз по оконному стеклу,— мгновенно бы прекратилось, если бы капля замерзла. Иными словами, то, что может быть доступно твердому телу только в случае, если ему придать форму сферы, капле доступно отнюдь не сферической, а расплющенной, потому что она жидкая.
Итак, капелька может двигаться между двумя поверхностями не механизмом качения, а механизмом переливания. При таком движении капли (оно наблюдается и у очень сплющенных капель) ее центр движется со скоростью вдвое меньшей, чем относительная скорость взаимного перемещения пластин. Это очень напоминает движение гусеничного трактора. Он движется со скоростью вдвое меньшей, чем скорость движения той части гусеничной ленты, которая не касается земли.
Еще одно важное свойство капель, укрепляющее идею каплеподшипников: с ростом давления, которое приложено к расплющенной капле, радиус жидкой лепешки растет медленно, лепешка упорно сопротивляется прилагаемой к ней нагрузке.