90. Вот как следует расположить семь человек:
Разумеется, за круглым столом А будет соседом человека, указанного в конце строки.
Первоначально я сформулировал эту задачу для 6 человек и 10 дней. Разумеется, легко видеть, что максимальное число расположений для n человек равно
. Эрнст Бергольт первым обнаружил сравнительно простой метод решения для всех случаев, где n равно простому числу + 1. Затем я указал способ построения решения для 10 человек, опираясь на который, Е. Д. Бьюли нашел общий метод для любых четных чисел. Нечетные числа, однако, оказались крайне трудными, и единственными нечетными числами, с которыми удалось справиться, были 7 (приведен выше), 5, 9, 17 и 33, причем четыре последних равны некой степени 2 плюс 1. Наконец, хотя и не без больших трудностей, я нашел некий тонкий метод решения для всех случаев и выписал схемы для всех чисел до 25 включительно. Для случая 11 решение получил также У. Нэш. Быть может, читатель испытает свои способности в случае 13. Он обнаружит, что это необычайно крепкий орешек.
91. Существует 12 способов расположения коробок без учета рисунков. Если бы все 13 рисунков были различны, то ответ оказался бы равен 93 312. Но поскольку в некоторых случаях коробки можно переставлять, не меняя расположения рисунков, число способов уменьшается на 1728, и, следовательно, коробки в соответствии с условиями можно расположить 91 584 способами. Я предоставляю моим читателям выяснить самостоятельно, как получаются эти числа.
92. Число способов, которыми можно разместить четырех поросят по 36 свинарникам в соответствии с заданными условиями, равно 17, включая приведенный мною пример и не считая новыми расположения, полученные из данных с помощью поворотов и отражений. Яниш в своей книге Analyse Mathematique au jeu des Echecs (1862 г.) утверждает, что существует 21 решение небольшой задачи, на которой основана данная головоломка. Поскольку я сам нашел только 17, то я вновь изучил этот вопрос и обнаружил, что он ошибается, несомненно, засчитав решения, полученные с помощью поворотов и отражений, за новые.
Вот 17 ответов. Цифры обозначают горизонтали, а их положение показывает вертикали. Так, например, 104 603 означает, что мы помещаем поросенка в первую строку и первый столбец, никого не помещаем во второй столбец, помещаем другого поросенка в четвертую строку и третий столбец, третьего — в шестую строку и четвертый столбец, никого — в пятый столбец, четвертого поросенка мы помещаем в третью строку и шестой столбец. Размещение Е я привел, формулируя условия:
Можно заметить, что N и Q полусимметричны относительно центра и, следовательно, с помощью поворотов и отражений породят лишь по 2 расположения каждое, что Н четвертьсимметрично и породит лишь 4 расположения, тогда как 14 других расположений породят с помощью поворотов и отражений по 8 расположений каждое. Следовательно, поворачивая и отражая данные 17 расположений, мы получим всего (2 × 2) + (4 × 1) + (8 × 14) = 120 способов.
Трех поросят можно поместить так, чтобы каждый свинарник располагался на одной прямой с поросенком при условии, что поросятам не запрещается располагаться на одной прямой с другими; но имеется только один способ сделать это (не считая поворотов и отражений), а именно: 105030.
93. Расположите кубики и знаки умножения следующим образом: 915 × 64 и 732 × 80; в обоих случаях произведение окажется равным максимально возможному числу 58 600.
94. Наименьшее возможное число ходов равно 22, то есть 11 для лис и 11 для гусей. Вот одно из решений головоломки:
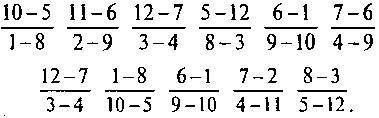
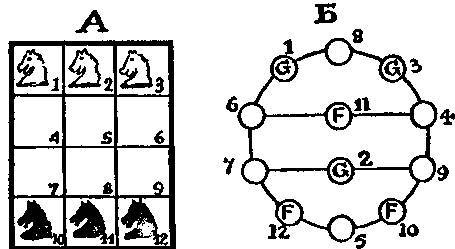
Разумеется, читатель должен сделать первый ход, указанный в числителе первой дроби, затем ход, указанный в знаменателе, затем ход, указанный в числителе второй дроби, и т. д. Я применю здесь мой метод «пуговиц и веревочек». На диаграмме А данная головоломка представлена на куске шахматной доски с шестью конями. Сравнение с рисунком из условия показывает, что там я избавил себя от необходимости объяснять неискушенному читателю, как ходит шахматный конь, проведя прямые, показывающие эти ходы. Так что эти две головоломки практически одно и то же, но в разных одеждах. Далее, сравнив рисунок из условия с диаграммой Б, можно заметить, что, расцепив «веревочки», соединяющие кружки, я упростил диаграмму, не изменив существенные соотношения между «пуговицами», или кружками. Читатель теперь без труда сам установит, что требуется 11 ходов для лис и 11 для гусей. Он заметит, что гусь с 1 или 3 должен ходить на 8, дабы избежать соседства с лисой и позволить лисе с 11 перейти на кольцо. Если мы пойдем 1— 8, то ясно, что для лис лучше ходить 10—5, а не 12— 5, когда все окажутся на окружности, то им нужно просто прогуляться вдоль нее по часовой стрелке, позаботившись сделать последними ходы 8—3 и 5—12. Таким образом, с помощью этого метода наша головоломка становится невероятно простой. (См. также замечание по поводу решения задачи 13.)
95. На рисунке показано, как из найденной доски можно вырезать два куска, из которых удается сложить квадратную крышку стола. А, В, С, D — углы стола. Способ, каким кусок Е вставляется в кусок F, должен быть очевидным для читателя. Заштрихованная часть удаляется.
96. Это число должно быть наименьшим общим кратным 1, 2, 3 и т. д. до 15, которое при делении на 7 дает остаток 1, на 9 — 3, на 11 — 10, на 13 — 3 и при делении на 14 дает остаток 8. Таким числом является 120. Следующее число с таким свойством — это 360 480, но поскольку не сохранилось свидетельств, чтобы одно дерево (да еще очень молодое) приносило когда-нибудь такое огромное количество яблок, единственным приемлемым ответом может быть лишь 120.
97. Прямоугольная закрытая цистерна, содержащая заданное количество воды и обладающая вместе с тем минимальной поверхностью, должна быть правильным кубом (то есть каждая ее сторона должна представлять собой квадрат). Для цистерны в 1000 кубических футов внутренние размеры должны быть 10×10×10 футов, а цинка на нее пойдет 600 квадратных футов. В случае цистерны без крышки пропорции будут точно как у полукуба. Это и есть требуемые «точные пропорции». Точные размеры привести нельзя, хотя близкими приближенными значениями будут 12,6 × 12,6 × 6,3 фута[36]. Цистерна с такими размерами будет содержать чуть больше воды, на что покупатель не станет жаловаться, а жестянщик затратит несущественное количество лишнего металла.
98. Если вы возьмете лист бумаги и проведете карандашом диагональную прямую, как на рисунке А, то, свернув из листа цилиндр так, чтобы карандашная линия оказалась снаружи, обнаружите, что эта линия будет выглядеть, как на рисунке Б.
Можно заметить, что длина спирали (за один полный оборот) равна длине гипотенузы прямоугольного треугольника, катетами которого служат два края листа. В данной головоломке длина этих катетов равна соответственно 40 фт (
от 200 фт) и 16 фт 8 дм = 16
фт.
Следовательно, гипотенуза равна 43
фт = 43 фт 4 дм, а значит, длина гирлянды в пять раз больше составляет 216 фт. 8 дм. Любопытная особенность этой головоломки состоит в том, что данное значение в точности совпадает с суммой высоты и окружности.