54. Решение этой головоломки лучше всего объяснить с помощью рисунка. Если шут положил свои 8 досок указанным здесь способом через угол, образованный канавой, то он сумел довольно просто перебраться через нее.

Таким образом королевский шут мог преодолеть все трудности и благополучно бежать, что он, как мам сообщает, и сделал.

КАК СОВЕРШАЛИСЬ РАЗЛИЧНЫЕ ТРЮКИ НА РОЖДЕСТВЕНСКОМ ВЕЧЕРЕ У СКВАЙРА

Запись одного из ежегодных «головоломных рождественских вечеров» у сквайра Дэвиджа, сделанная одной из юных родственниц этого старого джентльмена, которая часто проводила веселые рождественские праздники, в Стоук Коурси-Холле, не дает разгадки тайн. Поэтому я приведу мои собственные ответы на все головоломки и попытаюсь сделать их по возможности понятнее для тех, кто более или менее новичок в таких делах.

55. У мисс Чарити Локайер был, очевидно, в запасе какой-то трюк, и мне кажется, что скорее всего он состоял в следующем. Она предложила разложить десять кусков сахара по трем чашкам так, чтобы в каждой оказалось нечетное число кусков. На рисунке приведен возможный ответ, а цифры на чашках означают число кусков, положенных в каждую из них по отдельности. Помещая чашку, содержащую один кусок, в чашку, содержащую два куска, мы можем проверить, что действительно каждая из них содержит нечетное число кусков. В оставшейся чашке 7 (нечетное число) кусков. Итак, в одной чашке находится 1 кусок, во второй — 3 и в третьей — 7 кусков. Очевидно, что если чашка содержит другую чашку, то в ней находится и содержимое этой чашки.

Всего имеется пятнадцать различных решений этой головоломки:

Первые два числа в тройках показывают число кусков соответственно во внутренней и внешней чашках, вставленных друг в друга. Стоит отметить, что внешняя чашка этой пары сама по себе может быть пустой.

56. Трюк в данной головоломке заключался в следующем. Из одиннадцати монет удаляется пять, затем добавляются четыре монеты (к этим уже удаленным), и у вас получается девять монет — во второй кучке удаленных монет!

57. Фермер Роуз послал на рынок всего 101 гуся. Джейбз сначала продал мистеру Джасперу Тайлеру половину стада и половину гуся сверх того (то есть 50

+= 51, оставив 50 гусей); затем он продал фермеру Эйвенту треть остатка и еще треть гуся (то есть. 16+= 17, оставив 33 гуся); потом он продал вдове Фостер четверть остатка и еще три четверти гуся (то есть 8 + = 9 оставив 24 гуся); далее он продал Нэду Кольеру пятую часть остатка да еще подарил пятую часть гуся (то есть 4+ = 5, оставив 19 гусей). Этих 19 гусей он и привез назад.

58. Эта небольшая шутка майора Тренчарда также представляет собой головоломку с трюком, а плутовское выражение лица крайнего справа мальчика с цифрой 9 на спине ясно показывало, что он посвящен в тайну. Я не сомневаюсь (вспомните намек майора, что на числа надо «правильно смотреть»), что его ответ вы видите на рисунке, где мальчик 9 стоит на голове, отчего число на его спине превращается в 6. Это дает общую сумму 36 (четное число), так что, поменяв местами мальчиков 3 и 4 с 7 и 8, мы получаем 1, 2, 7, 8 и 5, 3, 4, 6, а это в каждом случае дает сумму, равную 18. Существуют три других разбиения мальчиков на группы, удовлетворяющих нужному условию: 1, 3, 6, 8 — 2, 4, 5, 7; 1, 4, 6, 7 — 2, 3, 5, 8 и 2, 3, 6, 7 — 1, 4, 5, 8.

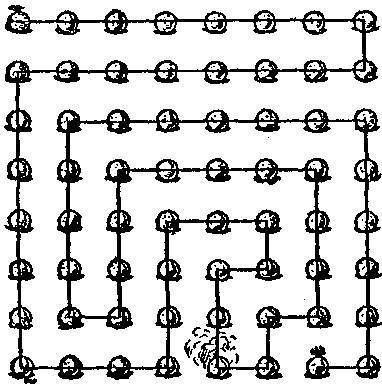
59. На рисунке показано решение данной головоломки. При наложенных условиях оно единственное. Начиная с верхнего пудинга, украшенного остролистом, мы касаемся всех пудингов за 21 прямолинейный проход, пробуя дымящийся пудинг в конце десятого прохода и заканчивая вторым пудингом, украшенным остролистом.

Здесь мы имеем пример невозвратного пути шахматной ладьи между максимально удаленными клетками. Ибо если бы мы пожелали посетить каждую клетку по одному и только одному разу, а начать и закончить путь в противоположных концах одной и той же диагонали, то это оказалось бы невозможным.

Существует довольно много различных путей от одного украшенного пудинга до другого с наименьшим числом (21) прямолинейных проходов, но я их не перечислил. Я записал 14 из них, а возможно, их еще больше. Любой из путей удовлетворяет всем условиям, кроме того, которое касается дымящегося пудинга. Это дополнительное условие было введено, дабы ликвидировать неоднозначность решения. Мне неизвестно какое-либо другое решение данной головоломки; однако, поскольку я не записал все решения без дополнительного условия, я не могу высказать в настоящее время категорического утверждения по этому вопросу.

60. Как оказалось, каждый из гостей поцеловал каждого под веткой омелы со следующими исключениями и дополнениями: ни одно лицо мужского пола не целовало лиц мужского пола; ни один женатый мужчина не целовал замужних женщин, кроме своей жены; все холостяки й мальчики поцеловали всех девушек и девочек дважды; вдовец не целовал никого; вдовы нс целовали друг друга. Каждый поцелуй возвращался и оба таких взаимных поцелуя считались за один. Составляя список всех присутствующих, мы можем удалить из него вдовца, ибо он выступал в роли наблюдателя.

7 женатых пар 14

3 вдовы 3

12 холостяков и мальчиков 12

10 девушек и девочек 10

Всего 39 человек

Далее: если бы каждый из 39 человек поцеловал всех остальных, то число поцелуев равнялось бы 741, а если бы 12 холостяков и мальчиков поцеловали 10 девушек и девочек еще по одному разу, то следовало бы добавить 120, что дало бы общее число поцелуев 861. Но поскольку ни один женатый мужчина не целовал замужних женщин, за исключением своей жены, мы должны вычесть 42 поцелуя; поскольку ни одно лицо мужского пола не целовало лиц мужского пола, мы должны вычесть еще 171 поцелуй; а поскольку ни одна вдова не целовала другую вдову, мы должны вычесть и еще 3 поцелуя. Следовательно, из общего числа 861 мы должны вычесть 42 + 171 + 13 = 216 поцелуев, что приводит к ответу: под веткой омелы всего было совершено 645 поцелуев.

61. Число различных кубов, объем которых в сумме составляет 17 кубических дюймов, бесконечно. Здесь приводятся наименьшие измерения. Ребро одного куба должно равняться 2

дюйма, а ребро другого дюйма.

Если читатель возьмет на себя труд возвести в куб каждое из этих чисел, то обнаружит, что сумма будет в точности равна 17. (См. также головоломку 20.)

ПРОИСШЕСТВИЯ В КЛУБЕ ГОЛОВОЛОМОК

62. Один за другим члены клуба находили ключ к тайне двусмысленной фотографии, только Чертой упорно предлагал сдаться. Тогда Герберт Бейнс привел доказательства того, что плащ, который нес на руке лорд Максфорд, был женским, ибо пуговицы на нем располагались на левой стороне, тогда как у мужского плаща они всегда находятся справа. Не похоже, чтобы лорд Максфорд гулял по парижским улицам с перекинутым через руку женским плащом, если бы он не сопровождал его владелицу. Следовательно, он шел вместе с леди.