Хью имеет степень доктора в области математики, а Боб много занимался математикой в колледже. Иными словами, мы оба провели кучу времени за изучением так называемых дифференциальных уравнений. Они казались нам невероятно скучными, но лишь до тех пор, пока мы не занялись изучением эффекта плато и не поняли, что именно дифференциальные уравнения – наиболее фундаментальный инструмент для решения трехмерных проблем в реальном мире – представляют собой математический способ для выражения этого эффекта. В сущности, дифференциальные уравнения относятся к эффекту плато так же, как E = mc² – к теории относительности. Высшая математика, которую иногда называют «божьим чертежом для вселенной», представляет собой язык плато. Мы покажем вам, что имеем в виду, и вам даже не понадобится калькулятор. На самом деле для объяснения вам понадобится собака.
Представьте, что вы хотите выстроить для своей собачки небольшой загон в саду у дома, чтобы она могла спокойно бегать перед ним по лужайке. Одна сторона загона – это стена вашего дома, так что вам нужно построить лишь три оставшиеся (легко!). Для еще большего упрощения задачи вы покупаете 15 метров готового забора, чтобы построить стороны под прямым углом (без кривых). Какая идеальная форма даст вашему Шарику максимальный объем пространства? Подсказка: мы не стали бы рассказывать вам эту историю, если бы в результате получился скучный квадрат.
Будь вы пещерным человеком, то, безусловно, допустили бы ошибку, пойдя экспериментальным путем. Ваша жена, возможно, утверждала бы, что стороны, граничащие с домом, должны быть длиннее, а вы возражали бы. Вы могли выстроить 50 различных конфигураций, а затем измерить параметры каждой из них. Не исключено, что после этого ваша жена, в бешенстве от того, что вы так долго возитесь с этой простой задачей, подала бы на развод.
Но вы можете решить эту проблему с помощью дифференциального уравнения примерно за 30 секунд. Судя по расчетам, идеальная форма представляет собой прямоугольник, длина двух сторон которого составляет половину от длины двух других – в данном случае сторона, параллельная дому, должна иметь длину 7,5 метра, а две другие – 3,75 метра (если вы хотите получить дополнительное подтверждение нашим расчетам, прочитайте текст сноски){6}.
Шарик получает реальную пользу от ваших расчетов. Если бы вы выбрали очевидную форму квадрата, то в его распоряжении было бы 25 квадратных метров. Однако, благодаря вашим развитым математическим навыкам он получает более 28 квадратных метров.
Реальный мир вокруг нас полон проблем, которые можно решить с помощью формул и расчетов. Вот вам проблема, с которой вы можете столкнуться буквально каждый день: как выглядит оптимальная форма для банки с прохладительным напитком, позволяющая максимизировать объем и при этом минимизировать площадь поверхности (а значит, сэкономить расходы на алюминий)? В сущности, это банка, высота которой чуть больше ширины. Но представьте, что вместо расчетов инженеры компаний – производителей колы тратили бы все время на досужие споры о том, выше или шире должны быть банки.
Кажется странным? Однако именно так большинство из нас проживает свою жизнь. Нам дают совет, и мы ему следуем. В течение какого-то времени все идет хорошо, но часто мы продолжаем следовать совету даже после того, как он пережил свою пользу. Давайте на минутку вернемся к истории с загоном для собаки и поясним, что мы имеем в виду.
Представьте себе, что вы начали строить квадратный загон, а ваша жена говорит, что вы должны удлинить сторону, противоположную дому. Она молодец, не правда ли? Правда, но лишь отчасти. Если бы вы последовали ее совету и удлинили сторону загона до предела, у собаки осталось бы меньше места, чем было. Что если бы упоенные властью конструкторы банок для напитков, которые хотели бы сделать их выше (назовем их высотчики), убедили производителя делать банки, напоминающие по форме миниатюрные небоскребы? Довольно быстро компания стала бы банкротом. Высотчики были правы, но лишь на время.
В решении проблем с загоном, формой банки и миллиона других проблем из реального мира имеется масса нюансов. Нужно учесть и это, и то, к тому же в разных пропорциях. Для поиска оптимального решения нужна высшая математика, однако большинство из нас пользуются лишь элементарной алгеброй. Подумайте хотя бы о политических дебатах – одна сторона кричит о снижении налогов, а другая – об инвестициях в инфраструктуру. Очевидно, что решение включает в себя результат балансирования между двумя идеями, однако республиканцам и демократам не так-то просто выйти за пределы выражения A + B = C. Одна сторона строит высокую и тонкую банку для напитков, а другая – банку, напоминающую по форме крышку канализационного люка. В результате страдаем мы все.
От такого алгебраического мышления в стиле «черное против белого» или «все или ничего» страдает множество сфер нашей жизни. Оно не позволяет нам ни сбросить вес, ни улучшить отношения, ни развить бизнес. Ведь диета работает, пока не перестает. И новая маркетинговая стратегия работает, пока не перестает. И вот что интересно: если бы вы испытали все возможные решения для собачьего загона, банки с кока-колой и любой другой проблемы из области реального мира, а затем нанесли варианты на график, то он имел бы такую форму:
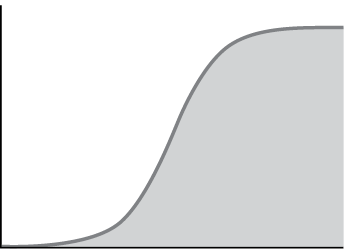
В момент, когда что-то достигнет оптимальной формы и размера, оно перестанет работать прежним образом, если вы продолжите применять прежнюю технику. Вот почему так важно пересматривать советы о диете, режиме спортивных упражнений или ведении бизнеса, которые вы получаете из книг, напичканных алгеброй. Мы предложим новый способ для оптимизации всех других советов. Люди, компании, мужья, жены и политические партии должны научиться основам вычислений, если только они действительно хотят решать проблемы в реальном трехмерном мире и избегать эффекта плато, вызванного, как ни странно, их вполне правильными действиями.
Желание быть правым – одна из самых мощных сил в истории человечества. Умные учителя давно усвоили, как использовать эту силу против (точнее, во благо) своих учеников. Хью получил немалое удовольствие от манипулирования высокомотивированными студентами, которых он обучал в Колумбийском университете. Они были идеальными подопытными морскими свинками. Как-то раз ему довелось читать довольно популярный курс в области информационных технологий в нью-йоркском кампусе одного из университетов Лиги плюща. В ходе лекции Хью рассматривал массу тем: почему ломаются системы, каким образом неумелое обращение приводит к тому, что базы данных теряют свой смысл. Рассказывал он и о том, почему людям часто кажется, что их личная информация может быть найдена и использована любым мошенником, и о том, каким образом хакеры смогли взломать коды иранской ядерной программы без единого выстрела. Также он проводил странные эксперименты, показывающие, насколько интересным (и вредным) может оказаться понимание сути данных. Как-то он попросил своих студентов активно использовать при общении в интернете выдуманное им выражение «отток контекста» (context reflux), чтобы проверить, сколько времени потребуется, чтобы это выражение прижилось в обиходной речи. К немалому восторгу студентов, уже после нескольких сообщений в блогах и твитов они начали замечать, как выражение «отток контекста» все чаще мелькает в поисковых запросах Google. Не исключено, что через какое-то время книга с названием типа «Отток контекста: революция в медиа» появится на полках магазинов. Сторонники и противники бывшего кандидата в президенты США Рика Санторума знают, насколько опасным может быть подобное «отравление» поисковых машин. На протяжении многих лет пользователи сети, проводившие поиск по слову Santorum, находили не информацию о бывшем сенаторе от Пенсильвании, а вульгарное и непристойное определение слова Santorum, запущенное в сеть противниками этого политика[5]. Данными легко манипулировать, и это даже может быть весело – если только вы не жертва.