[Дьюдени правильно показывает, что не более четырех областей можно нарисовать таким образом, чтобы каждая из них имела общий участок границы со всеми другими областями, но ему не удается доказать, что четырех красок будет достаточно для всех карт. Верно, что если любые четыре области на карте рассматривать изолированно, то для любой пятой области не потребуется пятой краски. Но ведь нужно доказать, что на любой карте с большим числом областей эти различные множества из пяти областей не вступят в конфликт друг с другом так, что потребуется пять красок [42].
Возникающую здесь трудность лучше всего можно заметить, если начать и в самом деле строить сложную карту, используя метод, предложенный Дьюдени. Если каждая новая область рисуется таким образом, чтобы она прилегала к трем другим областям, то соответствующая краска выбирается автоматически, и карту из четырех красок можно продолжить до бесконечности. Но если добавляются многие другие области, прилегающие только к одной, двум или вообще ни к одной из предыдущих областей, то выбор красок для этих областей становится произвольным. По мере того как карта увеличивается в размерах и становится все более запутанной, ее создатель неожиданно обнаруживает, что ему требуется пятая краска. Однако, вернувшись назад и изменив цвета предыдущих областей, можно, по-видимому, всегда исправить ошибку и обойтись четырьмя красками. Но в самом ли деле это возможно всегда? Вот что осталось недоказанным. Относительно дискуссии по этой проблеме и ссылок на недавние работы см. гл. 43, посвященную проблеме четырех красок, в моей книге «Математические головоломки и развлечения» (М., изд-во «Мир», 1971). — М. Г.]
432. Две! Требуются четыре цвета. Если у мальчика в ящике имеется лишь три краски (красная, голубая и желтая), то он может получить оранжевый, зеленый и фиолетовый цвета, смешивая их между собой. Но он не может получить четыре цвета менее, чем из трех красок. Следовательно, у него в ящике две краски («не хватает одной краски»). «Цветом» считается красный, оранжевый, желтый, зеленый, голубой или фиолетовый. Различные оттенки, вроде голубовато-зеленого или желто-зеленого, не допускаются.
433. Умножьте 2 столько раз на себя, сколько всего картин, и вычтите 1. Так, 2 в десятой степени равно 1024. Вычитая 1, мы получаем 1023 — правильный ответ. Предположим, что у нас только три картины. Тогда одну из них можно выбрать тремя способами, две — тоже тремя способами и три — одним, что в сумме дает 7 способов. Но 7 как раз и равняется 2 3- 1 [43].
434. Всего имеется 39 147 416 разных способов. Прибавьте 3 к числу членов (что даст 618) и вычтите 1 из числа партий (что даст 3). Тогда ответом будет число способов, которыми можно выбрать 3 предмета из 618, то есть
Общее решение таково. Пусть p — число партий, а m — число членов парламента. Число способов равно числу сочетаний из m+ p- 1 объектов по p- 1.
435. Если нет никаких ограничений, то 10 человек могут разместиться на прямой 10! = 3 628 800 способами. Сколько из этих перестановок запрещено? Будем рассматривать двух человек одной национальности, заключенных в скобки, как единое целое.
1. Тогда (Ан, Аи) (Ш, Ш) (У, У) Ф Ит Ис Ам можно переставить 7! × 2 3= 40 320 способами. Помните, что два Ан могут меняться местами внутри скобок, где бы последние ни расположились, и то же самое верно для Ш и У. Отсюда и появляется 2 3.
2. Однако мы можем рассмотреть (Ан, Ан) (Ш, Ш) У У Ф Ит Ис Ам, где два У не объединены скобками, а «свободны». Это даст нам 8! × 2 2вариантов, но мы должны исключить отсюда результат пункта 1, чтобы не сосчитать некоторые перестановки дважды. Получаем 120 960.
3. Поступим аналогичным образом с двумя «свободными» Ш. Получим 120 960.
4. Поступим так же с двумя «свободными» Ан. Получим 120 960.
5. Но мы можем рассмотреть (Ан, Ан) Ш Ш У У Ф Ит Ис Ам, где и Ш, и У «свободны». Это даст нам 9! × 2 случаев, из которых мы должны вычесть результаты пунктов 1, 2 и 3 по очевидным теперь причинам. Получим 443 520.
6. Когда в скобки заключены только Ш, вычтем результаты пунктов 1, 2 и 4. Получим 443 520.
7. Когда в скобках оставлены только У, вычтем результаты пунктов 1, 3 и 4. Получим 443 520.
Сложим результаты семи пунктов и получим при этом 1 733 760. Теперь из самого первого результата вычтем полученное число, что даст нам верный ответ, равный 1 895 040 способам.
436. Головоломку можно решить за 9 переправ следующим образом:
1) мистер и миссис Вебстер переправляются вместе;
2) миссис Вебстер возвращается;
3) переправляются мать и невестка;
4) возвращается мистер Вебстер;
5) переправляются тесть и сын;
6) возвращается невестка;
7) переправляются мистер Вебстер с невесткой;
8) возвращается мистер Вебстер;
9) мистер и миссис Вебстер переправляются вместе.
437. Обозначим трех миссионеров через М м м, а трех каннибалов через К к к; прописными буквами обозначены миссионер и каннибал, умеющие грести. Тогда переправляются К к; К возвращается на лодке; переправляются К к; К возвращается; переправляются М м; возвращаются М к; переправляются М К; возвращаются М к; переправляются М м; возвращается К; переправляются К к; К возвращается; переправляются К к; при этом все переправляются через реку, не нарушая заданных условий.
[Задачи о переправах через реку этого и предыдущего типа решаются с помощью простого метода из теории графов. См. гл. 35 книги М. Гарднера «Математические досуги» (М., изд-во «Мир», 1972). — М. Г.]
438. Двое детей гребут к другому берегу. Один из них вылезает, а другой возвращается назад. Один солдат переправляется, вылезает, а мальчик возвращается назад. Таким образом, чтобы переправить на другой берег одного взрослого, лодка должна 4 раза проплыть от берега до берега. Поэтому ей пришлось сделать 4 × 358 = 1432 рейса, чтобы переправить офицера и 357 солдат, причем лодка в конце концов снова оказалась у детей.
439. Можно составить следующую таблицу:
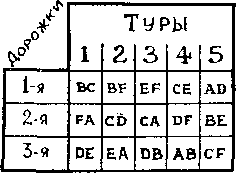
440. Из таблицы можно сразу определить, что Англия победила Ирландию и сыграла вничью с Уэльсом. Поскольку А сыграла в этих матчах с общим счетом 2 : 0, то она должна была победить со счетом 2 : 0, а вничью сыграть со счетом 0 : 0. Таким образом, нам все известно про А и остается только определить результаты трех матчей: У с И, Ш с И и Ш с У. Шотландия пропустила только 1 гол от У или И. И забила только 1 гол в ворота У или Ш. Допустим, что в ворота Ш. Тогда У не забил ни одного гола в ворота Ш. Но У всего забил 3 гола; следовательно, все они были забиты в ворота И. Получается, что в ворота И было забито 6 голов: 2 — А, 3 — У (если принять, что И забила гол в ворота Ш) и оставшийся гол — Ш. Но поскольку мы приняли, что И забила 1 гол в ворота Ш, матч между этими командами должен был закончиться вничью. Однако из таблицы видно, что в этом матче выиграла Ш и, следовательно, И не могла забить гол в ворота Ш. Таким образом, гол в ворота Ш забил У. А поскольку У всего забил 3 гола, то остальные 2 были забиты в ворота И, которая свой единственный гол забила в ворота У. Окончательно мы получаем, что Ш выиграла у У со счетом 2 : 1, у И со счетом 2 : 0, а У выиграл у И со счетом 2 : 1.
441. Пусть 8 делений разбивают 33-сантиметровую линейку на 9 частей длиной 1, 3, 1, 9, 2, 7, 2, 6, 2 см. Тогда с их помощью можно измерить любое целое число сантиметров от 1 до 33 см. Разумеется, сами деления находятся на расстояниях 1, 4, 5, 14, 16, 23, 25 и 31 см от одного из концов линейки. Другим решением будет 1, 1, 1, 1, 6. 6, 6, 6, 5 см.
Эта головоломка имеет по крайней мере 16 решений. Я нашел правило, с помощью которого можно определять минимальное число делений для линеек любой длины и выписывать некоторые решения, однако общий закон, которому подчиняются все решения, еще не найден.