241. Сторона одного участка составляет 38 м (1444 плиты), сторона другого — 26 м (676 плит).

242. Всего было 180 колонок, а длина всей линии, окружающей памятник, составляла 33 м. Если ставить колонки через 10 см, тогда не хватит 150 колонок, а если ставить их через 30 см, то будет достаточно 110 и еще 70 колонок останется.

243. Сначала мы находим возраст обезьяны (1½ года) и возраст ее матери (2½ года). Следовательно, обезьяна весит 2½ фунта и столько же весит груз. Затем мы находим, что вес веревки составляет 1¼ фунта, или 20 унций, а поскольку каждый фут весит 4 унции, то длина веревки равна 5 футам.

244. Всего было 900 человек. Первоначально выехало 100 фургонов по 9 человек в каждом. После того как сломалось 10 фургонов, в оставшихся оказалось по 10 человек («по одному лишнему человеку»). Когда при отправке домой сломалось еще 15 фургонов, в каждом из 75 оставшихся фургонов ехало по 12 человек («на три человека больше, чем было во время отъезда утром»).

245. Пэт сказал: «Какое число ни назови, все едино, а раз тут десять человек да еще я сам, то назову-ка я одиннадцать и начну счет с себя». Разумеется, первым отправился на порку он сам. Следовательно, если начинать с номера 1, то наименьшим числом, роковым для англичан, будет 11. На самом деле Пэту следовало назвать 29 и начинать счет с номера 9. Тогда экзекуции подверглись бы все носильщики. Эти два числа минимальны.

246. Бакалейщик должен смешать 70 фунтов чая по 32 цента и 30 фунтов чая по 40 центов за фунт.

247. Рыба весит 72 унции, или 4½ фунта. Хвост весит 9 унций, туловище 36 и голова 27 унций.

248. Ясно, что 999 919 не может быть простым числом и что, поскольку нужно найти единственное решение, оно должно разлагаться в произведение двух простых сомножителей. Этими сомножителями будут 991 и 1009. Нам известно, что каждая кошка поймала больше мышек, чем было кошек. Значит, всего была 991 кошка, и каждая из них поймала по 1009 мышек.

249. Пусть номер ящика равен n. Тогда в нем будет 2 n- 1 перегородок в одном направлении и 2 n- 3 в другом, что даст 4 n ²- 4 nячеек и 4 n- 4 перегородок. Так, в двенадцатом ящике имеются 23 и 21 перегородок (всего 44) и 528 ячеек. Это правило годится для всех ящиков, кроме второго, где может быть любое количество перегородок в одном направлении и одна перегородка в другом. Так что 1 и 1 подойдут (единственная перегородка не годится, поскольку такое «перегораживание» было бы нелепостью). Таким образом, всего получается 262 перегородки и 2284 ячейки (а не 264 и 2288).

250. Если внутренний диаметр звена умножить на число звеньев и прибавить удвоенную толщину железного прута, то получится длина цепи. Каждое звено, присоединенное к цепи, теряет в своей длине удвоенную толщину прута. Внутренний диаметр равен 2⅓ см. Если мы умножим его на 9 и прибавим 1, то получим ровно 22 см, а если мы умножим его на 15 и прибавим 1, то как раз и получится 36 см. Следовательно, два куска цепи содержат соответственно по 9 и 15 звеньев.

251. Если брат отвечал Доре «чет», то десятицентовая монета находилась в правом кармане, а пятицентовая в левом. Если же он говорил «нечет», то пятицентовая монета лежала в правом, а десятицентовая в левом кармане.

252. Первоначально в каждой сахарнице было по 36 кусков, а после того, как в каждую чашку положили по 2 (

) куска, в чашках стало по 6, а в сахарницах — по 18 кусков. Разность как раз и равна 12.

253. Всего 51 секция, в каждой секции по 23 целые колонки. Итого получалось 1173 целые колонки и 50 пар половинок, что составляло в совокупности 1223 колонки, как и требовалось по условию задачи.

254. Пусть длина AB10 см. Из точки Bвосставим к ABперпендикуляр BC, равный половине AB. Соединим точки Aи Cотрезком прямой и продолжим его за точку Cтак, чтобы CD= CB. Проведем отрезок BD. Это и есть искомый радиус окружности. Если начертить эту окружность и вписать в нее правильный пятиугольник, то стороны последнего будут точно равны 10 см.

255. Чтобы отметить вершины квадрата с помощью одного циркуля, сначала рисуют круг. Затем, зафиксировав раствор циркуля и начав с любой произвольно взятой на окружности точки A, отмечают точки B, Cи D. Из точек Aи Dкак из центров раствором ACописывают две дуги, пересекающиеся в точке E. Расстояние EOравно стороне искомого квадрата. Следовательно, если мы сделаем из Aзасечки Fи Gрадиусом OE, то A, F, D, Gи будут искомыми вершинами квадрата.

256. Если провести 15 прямых так, как показано на рисунке, получится ровно 100 квадратов. У сорока из них сторона равна AB, у двадцати — AC, у восемнадцати — AD, у десяти — AEи у четырех — AF. С помощью 15 прямых можно образовать даже 112 квадратов, но от нас требовалось точно 100. С помощью 14 прямых вам не удастся построить более 91 квадрата.

В общем случае с помощью nпрямых можно образовать ( n- 3)( n- 1)( n+ 1)/24 квадратов, если nнечетно, и ( n- 2) n( n- 1)/24 квадратов, если nчетно.

Если мы имеем mпрямых, перпендикулярных другим nпрямым, причем mменьше n, то число квадратов равно

257. Правило заключается в следующем. Если четыре стороны образуют арифметическую прогрессию, то наибольшая площадь равна квадратному корню из произведения всех сторон. Квадратный корень из 70 × 80 × 90 × 100 равен 7099 м ². Это и есть верный ответ.

258. Площадь дорожки равна точно 66⅔ м ², что станет совершенно очевидным, если вы представите себе маленький треугольный кусок, отрезанный снизу и перенесенный в правый верхний угол (см. рисунок).

Докажем наше утверждение. Площадь всего сада равна 55 × 40 = 2200 м ². Но (53⅓ × 40) + 66⅔ также равно 2200. Кроме того, сумма чисел

²и 40 ²должна равняться ², что и выполняется в действительности.

Общее решение таково. Обозначим ширину прямоугольника через B, длину через L, ширину дорожки через Cи длину дорожки через x. Тогда

В нашем случае x= 66⅔; следовательно, основание прямоугольного треугольника с гипотенузой 66⅔ м и катетом, равным 40 м, составляет 53⅓ м.

259. Разделим стороны треугольника точками A, Bи Eпополам. Если провести ABи опустить перпендикуляры DAи CB, то ABCDбудет наибольшим возможным прямоугольником, а его площадь составит половину площади треугольника. Два других решения FEAGи KEBHподошли бы нам (у обоих та же самая площадь), если бы они не захватывали дерево. Это правило можно приложить к любому остроугольному треугольнику, а в случае прямоугольного треугольника получатся только два решения.

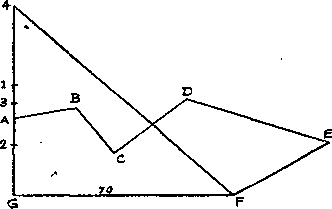
260. Многоугольник с произвольным числом сторон можно свести к равновеликому треугольнику, а поскольку угол AGFоказался прямым, то сделать это очень легко. Продолжим отрезок GA. Приложим линейку к точкам Aи C, параллельно перенесем ее вверх до точки Bи отметим точку 1. Затем соединим отрезком прямой точки 1 и Dи параллельно перенесем его вверх до точки C, отметив точку 2. Теперь приложим линейку к точкам 2 и E, параллельно перенесем ее до точки Dи отметим точку 3. Далее соединим линейкой точки 3 и F, параллельно перенесем ее до E, отметив точку 4. Если теперь мы соединим прямой точки 4 и Fто получим треугольник G4 F, площадь которого равна площади нашего неправильного поля. Поскольку на карте GFравно 7 см (70 м), то отрезок G4 равен 6 см (60 м) и площадь поля равна ½(70 × 60), или 2100 м ². Этот простой и ценный способ определения площади многоугольников следовало бы знать каждому, но, увы, пока это остается лишь благим пожеланием.