71. Утверждение о равенстве средних скоростей ошибочно. В действительности средние скорости кораблей не равны. Первый корабль проходит милю за

ч в одном направлении и за ⅛ ч в обратном. Полусумма этих дробей равна . Следовательно, средняя скорость, с которой первый корабль проходит 400 миль, равна 1 миле за ч. Средняя скорость второго корабля составляет 1 милю за ч.

72. Расстояние между двумя пунктами равно 18 км. Точки встречи отстоят от Aи Bна 10 и 12 км соответственно. Умножьте 10 (первое расстояние) на 3 и вычтите второе расстояние — 12. Что может быть проще? Испробуйте другие расстояния до точек встречи (следя за тем, чтобы первое расстояние составляло более ⅔ второго) и вы обнаружите, что это правило действует с неизменным успехом.

73. Собака бежала со скоростью 16 км/ч. Ключом к решению задачи служат следующие рассуждения. Расстояние, которое человеку осталось пройти рядом с собакой, составляло 81 м, или 3 ⁴(пес возвращался 4 раза), а длина дорожки равнялась 625 м, или 5 ⁴. Поэтому разность скоростей (выраженных в км/ч) человека и собаки (то есть 12) и сумма их скоростей (20) должны находиться в отношении 3 : 5.

74. Вполне очевидно, что Бакстер догонит Андерсона через один час, поскольку к этому времени они пройдут по 4 км в одном направлении. Далее, скорость собаки составляет 10 км/ч; следовательно, за этот час она пробежит 10 км! Когда эту головоломку предложили одному французскому профессору математики, тот воскликнул: «Mon Dieu, quelle sґerie!», [31]совершенно не заметив, как просто она решается.

75. Девять исследователей A, B, C, D, E, F, G, H, Jпроезжают 40 миль, затратив на это по полному баку горючего. Затем Aпередает по 1 галлону остальным восьми участникам и поворачивает назад, причем у него остается 1 галлон на обратную дорогу. Остальные восемь участников едут еще 40 миль, затем Bпередает по 1 галлону семи другим исследователям. Двух галлонов ему как раз хватает на обратный путь. Семеро исследователей проезжают еще 40 миль, затем Cпередает остальным шести по 1 галлону и возвращается домой, затратив на обратный путь 3 галлона. Шестеро исследователей проезжают еще 40 миль, после чего Dпередает каждому по 1 галлону и возвращается назад. Пятеро оставшихся проезжают еще 40 миль, затем Eдает каждому по 1 галлону и возвращается назад. Теперь уже четверо исследователей продвигаются еще на 40 миль в глубь пустыни, Fраздает каждому по 1 галлону и возвращается назад. G, H, Jпреодолевают еще 40 миль, Gдает каждому по 1 галлону и едет назад. Hи Jпроезжают еще 40 миль, Hотдает 1 галлон Jи возвращается. Наконец, последний путешественник Jпроезжает еще 40 миль, располагая 9 галлонами на обратный путь. Таким образом, Jдостигает пункта, расположенного в 360 милях от начального. Это наибольшее расстояние, которое можно проехать по прямой при заданных условиях.

76. Уокинхолм складывает 5 рационов на 90-мильной отметке (см. рисунок) и возвращается на базу (5 дней). Затем он оставляет 1 рацион на отметке 85 миль и возвращается к отметке 90 миль (1 день). Один рацион профессор оставляет на отметке 80 миль и возвращается снова к отметке 90 миль (1 день). Переносит 1 рацион на отметку 80 миль, возвращается к отметке 85 миль, подбирает оставшийся там 1 рацион и переносит его на отметку 80 миль (1 день). «Забрасывает» 1 рацион на отметку 70 миль и возвращается к отметке 80 миль (1 день), затем возвращается на базу (1 день). Таким образом, на отметках 70 и 90 миль остается по 1 рациону. Уокинхолм переносит 1 рацион на отметку 5 миль и возвращается на базу (1 день). Если ему нужно пройти 20 миль, то он может это сделать, дойдя до отметки 10 миль и вернувшись на базу. Переносит 4 рациона на отметку 10 миль и возвращается на базу (4 дня). Оставляет 1 рацион на отметке 10 миль и возвращается к отметке 5 миль, подбирает оставленный там 1 рацион и переносит его к отметке 10 миль (1 день). Переносит 2 рациона на отметку 20 миль и возвращается к отметке 10 миль (2 дня). Переносит 1 рацион к отметке 25 миль и возвращается к отметке 20 миль (1 день). Оставляет 1 рацион на отметке 30 миль, возвращается к отметке 25 миль, забирает оставленный там 1 рацион и переносит его на отметку 30 миль (1 день). Идет к отметке 70 миль (2 дня). Идет на базу (1½ дня). Всего 23½ дня.

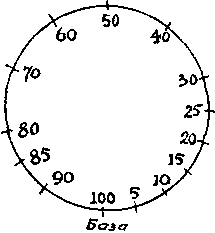
Предпринимались попытки уменьшить это время, но все они были основаны на трюках, так или иначе запрещенных. Например, Уокинхолма «вынуждали» оставлять не целый суточный рацион, а лишь его часть, совершать марш-бросок или съедать суточный рацион перед уходом с очередной отметки, чтобы он мог нести еще два суточных рациона и т. п. В последнем случае Уокинхолм на самом деле нес бы три рациона: один в желудке и два за плечами!

Если бы маршрут профессора пролегал по пустыне, то кратчайшее время равнялось бы 86 дням, а поступать следовало бы так.

Сложить 42 рациона в 10 милях от базы, вернуться на базу (42 дня). Отнести 1 рацион на отметку 15 миль, вернуться к первому складу в 10 милях от базы (1 день). Оставить 20 рационов в 20 милях от базы и вернуться к складу, расположенному в 10 милях от базы (20 дней). Отнести 1 рацион на расстояние 20 миль от базы и вернуться в точку, отстоящую на 15 миль от базы, взять ранее оставленный там 1 рацион и перенести его к отметке 20 миль (1 день). Перенести 10 рационов в точку, отстоящую на 30 миль от базы, и вернуться к отметке 20 миль (10 дней). Отнести 1 рацион к отметке 35 миль и вернуться к отметке 30 миль (1 день). Отнести 4 рациона на отметку 40 миль и вернуться к отметке 30 миль (4 дня). Отнести 1 рацион к отметке 40 миль и вернуться к отметке 35 миль. Взять там 1 рацион и перенести его к отметке 40 миль (1 день). Отнести 2 рациона в точку, отстоящую на 50 миль от базы, и вернуться к отметке 40 миль (2 дня). Отнести 1 рацион к отметке 55 миль и вернуться к отметке 50 миль (1 день). Перенести 1 рацион к отметке 60 миль и вернуться к отметке 55 миль. Взять там 1 рацион и перенести его на отметку 60 миль (1 день). Совершить оттуда переход до конечного пункта маршрута (2 дня). Всего — 86 дней.

77. Если человек, выйдя из A, пройдет 1⅔ км со скоростью 5 км/ч, то на это он затратит 20 мин. Обратный путь со скоростью 4 км/ч займет у приятелей 25 мин. Таким образом, человек догонит приятеля-инвалида в 12.35. Последний к тому времени проедет ⅔ км за 35 мин со скоростью 1

км/ч.

78. Предположим, что поезд идет в течение часа и имеет невероятную длину 3 км. Тогда (см. рисунок) за это время он пройдет от Bдо C60 км, а пассажир переместится от Aдо C, или на 63 км. С другой стороны, если бы пассажир шел от паровоза в хвост поезда, то поезд успел бы пройти расстояние от Bдо C(снова 60 км), в то время как пассажир переместился бы лишь на расстояние от Bдо C, то есть на 57 км. Следовательно,в первом случае скорость пассажира относительно железнодорожного полотна составляет 63, а во втором — 57 км/ч [32].

79. Поскольку поезд идет 5 ч, разделим путь на 5 равных интервалов. Когда леди выезжает из Вюрцльтауна, 4 встречных поезда уже находятся в пути, а пятый лишь отправляется со станции. Каждый из этих 5 поездов она встретит. Когда леди проедет ⅕ пути, из Мадвилля отправится новый встречный поезд, когда она проедет ⅖ пути — еще один, ⅗ — еще один, ⅘ — еще один и, наконец, когда она прибудет в Мадвилль, оттуда как раз будет отправляться очередной, пятый, поезд. Если мы примем, как и следует сделать, что она не встречает «по пути» ни этот последний поезд, ни тот, который прибыл в Вюрцльтаун, когда ее поезд отправлялся оттуда, то по дороге из Вюрцльтауна в Мадвилль леди повстречает 9 поездов.