Если мы обратим внимание на то, что в эвклидовской сферической тригонометрии сферический треугольник есть не что иное, как трехгранный угол с вершиной в центре шара и сторонами, равными дугам больших кругов, то можно будет сказать, что прямолинейная эллиптическая тригонометрия вполне тождественна с эвклидовской сферической тригонометрией. Если наши отвлеченно–идеальные фигуры будут воплощены на поверхности шара, но в то же время будут квалифицироваться не как явления на поверхности, а как явления на плоскости, то мы и получим эллиптическую геометрию. Этим фигурам будет свойственна любая выразительная кривизна, зависящая не от них самих, но от непосредственного отождествления их с чистым и пустым, абсолютно алогичным инобытием–пространством.

Наконец, из основных геометрических свойств анализируемой плоскости я бы указал еще на одно, может быть, самое замечательное, что здесь имеется. Именно, эллиптическая плоскость односторонней. И чтобы это понять, тут тоже необходимо полететь «вверх пятами», но только на этот раз уже в буквальном смысле. Можно ли себе представить, что плоскость не имеет двух сторон, например верхней и нижней? Казалось бы, это есть уже какое–то умопомешательство. А тем не менее это надо себе представить, так как настоящая математика вообще есть ниспровержение «здравого рассудка», хотя людская пошлость сумела и здесь поставить все вверх дном и понять математику именно как апофеоз здравого рассудка. Но что же это такое, односторонняя плоскость, или поверхность? Укажем сначала ее философское место и потом приведем и геометрический образ.

Мы знаем: всякая прямая имеет только одну бесконечно удаленную точку, что указывает на тождество положительного и отрицательного направления в смысле достижения этой точки. Мы знаем также, что в эвклидов–ском пространстве две параллельные встречаются в бесконечно удаленной точке, как бы изгибаясь одна другой навстречу. Но представим себе некую фигуру между этими двумя параллельными. Если верхняя параллельная склоняется книзу ^[79], а нижняя кверху, то, очевидно, фигура, заключенная между параллельными, перевертывается, прохождение через бесконечно удаленную область сопровождается перевертыванием. То, что в конечной области есть верх, то в бесконечности — низ, а что низ, то — верх. Поверхность, проходящая через бесконечно удаленную область, выворачивается наизнанку, гак что уже нельзя различить, где лицо и где изнанка. Таким образом, односторонность поверхности есть в философском смысле не больше как уход в инобытие, где уходящее отрицает самого себя, но где оно одновременно и находит себя, отождествляется с собою. Одна и та же философская идея заключается и в том, что прямая имеет только одну бесконечно удаленную точку, т. е. что направления тождественны, и в том, что фигура, проходящая через бесконечно удаленную точку, перевертывается, и в том, что эллиптическая плоскость одностороння. Ведь последняя есть символ бесконечности, т. е. она воплощает бесконечные отношения в конечной и, следовательно, выразительной форме. Поэтому то, что у Эвклида осуществляется только при условии предельного процесса, в геометрии Римана происходит уже в конечной области.

Яснее всего односторонняя поверхность представима на поверхности Мёбиуса [рис. 6 ] ^[80]. Если в одной точке этой поверхности мы поместим и заведем часы, то, когда они пройдут всю эту поверхность и вернутся к исходной точке, мы заметим, что их стрелка движется теперь уже в обратную сторону. Если по средней линии поверхности Мёбиуса пройдет река, то мы, двигаясь вдоль одного берега, рано или поздно очутимся на другом берегу, хотя и без всякого переплывания с одного берега на другой по воде. Эти чудеса, творящиеся в эллиптическом пространстве, математически объяснимы слишком элементарно, чтобы можно было удивляться (идея односторонней поверхности), философски же это есть только логически последовательно проведенная идея бесконечности.

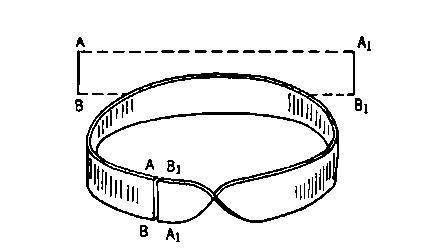
Однородность поверхности вполне ясна и на связке прямых. Если эти прямые образуют конус и его ось мы повернем на 180°, то образующая, которая раньше описывала коническую поверхность в одном направлении, теперь будет описывать ее в обратном, что и есть признак односторонности.

6. В настоящем контексте мы не будем подробно рассматривать виды выразительного пространства и ограничимся лишь краткими замечаниями.

a) Во–первых, пространство Римана может быть только эллиптическим. Когда мыслится, что всякая прямая пересекается с другой прямой не в одной, а в двух точках, мы получаем не эллиптическую Риманову, но сферическую Риманову геометрию. Используя нашу сеть сфер, мы теперь должны пару точек сети принимать не за одну точку, как в эллиптическом пространстве, но за две взаимно сопряженные точки. То же самое мы получим, если в качестве пра–символа сферического пространства возьмем связку лучей (вместо связки полных прямых). Тогда, по аналогии с эллиптическим пространством, точкой будет луч связки, прямой — плоскость связки, плоскостью— вся связка, отрезком — угол между двумя лучами, углом на плоскости — трехгранный угол и т. д. Если же мы из центра связки лучей опишем шаровую поверхность радиусом = 1 и установим взаимно однозначное соответствие между лучами связки и точками поверхности, то полученная геометрия на поверхности шара будет полным пра–символом сферической планиметрии — стоит только под точкой понимать точку обязательно шаровой поверхности, под взаимно сопряженными точками—диаметрально противоположные, под прямой — окружность большого круга, под плоскостью — поверхность шара, под отрезком—дугу большого круга, под углом — угол между окружностями больших кругов и иод треугольником — сферический треугольник. При всем сходстве с эллиптической системой тут и большие различия— вроде, например, того, что сферическая плоскость—двухсторонняя (она тут как бы дважды выворачивается и потому остается в первоначальном виде) или что полный угол составляет тут не два, а четыре прямых и т. д.

Если разница между обеими геометриями Римана есть разница геометрий связки прямых и связки лучей, то для прямой в одной связке мы находим два луча в другой и, следовательно, фигура в одном пространстве соответствует двум симметричным фигурам в другом пространстве, что каждой точке и двум прямым эллиптической плоскости соответствуют две различные, взаимно противоположные точки и две прямые с двумя общими точками сферической плоскости или что, вообще говоря, эллиптическая плоскость двойная ^[81].

b) Обеим Римановым геометриям противостоит геометрия Лобачевского, «гиперболическая». Ее пра–сим–вол — указанная выше гиперболическая связка окружностей. Тут мы находим бесчисленное количество окружностей и сфер, которые не пересекаются с данной окружностью или сферой. Можно сказать, что непересекающиеся окружности пересекаются здесь в мнимых точках, а две непересекающиеся сферы имеют общую мнимую окружность, которую всякая прямая, проходящая через точку О в этой плоскости, пересекает в двух взаимно обратных мнимых точках. Вместо того чтобы всем прямым пересекаться уже на конечном расстоянии, мы находим тут целых три категории взаимоотношения прямых. Две прямые определяют здесь или пучок сходящихся прямых (это есть и у Римана, и у Эвклида), или пучок параллельных прямых (как у Эвклида), или пучок расходящихся прямых. Последние и есть оригинальность плоскости Лобачевского. Этот пучок есть совокупность прямых, перпендикулярных к общему перпендикуляру двух данных прямых. Расстояние между двумя параллелями беспредельно растет в одном направлении и беспредельно убывает в противоположном. Поэтому происходит непрерывный переход от пересекающихся, сходящихся прямых через параллели к расходящимся. Если у Римана вовсе нет вещественных бесконечно удаленных точек <…> так что они пересекают эту область, но все еще не пересекаются в ней, а пересекаются где–то за ней, мнимо.