Оптическую иллюзию, изображенную на рис. 11 и 12, первым описал Иоганн Цёлльнер. Он случайно заметил этот эффект на рисунке ткани. Длинные параллельные прямые на рис. 11 кажутся расходящимися, а на рис. 12 — сходящимися.

Картинка, демонстрирующая так называемую иллюзию Херинга (рис. 13), была впервые опубликована Эвальдом Херингом в 1861 г.: горизонтальные прямые кажутся здесь изогнутыми на фоне сходящихся наклонных прямых.

Ненадежность зрения подтверждается еще одним примером, придуманным С. Толанским. На рис. 14 изображена фигура, обычно встречающаяся в работах но статистике. Основание CDфигуры равно ее высоте. Если попросить зрителя провести отрезок, равный полуширине (половине CD) фигуры, то он, как правило, проводит отрезок AB,тогда как в действительности полуширине равен отрезок XY.

Нам всем хорошо знакома иллюзия, используемая широко, сознательно и высокопрофессионально, а именно реалистическая живопись. Художник намеренно пытается изобразить трехмерную сцену на плоском (двумерном) холсте. Одно из великих достижений художников эпохи Возрождения заключалось в создании математической схемы, известной под названием теории линейной перспективы, которая позволяет добиться желаемого эффекта.

С некоторыми простыми примерами иллюзии, рожденной линейной перспективой, мы встречаемся в своем повседневном опыте. Принцип, используемый в этих примерах и в теории линейной перспективы, состоит в том, что линии в реальной сцене, идущие от зрителя, должны казаться сходящимися в некоторой точке — так называемой точке схода. Простым примером могут служить два параллельных рельса железной дороги: кажется, что они сходятся-вдали в некоторой точке (рис. 15).

Эффект перспективы особенно заметен на рис. 16, где лучи, идущие в точку схода, проведены для создания иллюзии объемной сцены. Высокие ящики в действительности одинаковы (имеют одну и ту же длину, ширину и высоту), но кажется, что «дальний» ящик больше. Опыт говорит, что с увеличением расстояния до наблюдаемого предмета его размеры кажутся меньше, поэтому правый ящик выглядит больше, чем на самом деле.

Питая горячее пристрастие к реалистической живописи, мы охотно идем на то, чтобы быть обманутыми. Более того, этот обман доставляет нам удовольствие. Написанные в реалистической манере картины двумерны, но если они нарисованы в соответствии с законами математической теории линейной перспективы, то, глядя на них, мы испытываем такое ощущение, будто разглядываем трехмерную сцену. Хорошим примером такого рода «объемных изображений» может служить «Афинская академия» Рафаэля (рис. 17).

Резюмируя, мы можем утверждать, что математическая теория линейной перспективы позволяет использовать оптические иллюзии. Изображая на заднем плане предметы и человеческие фигуры меньших размеров, чем на переднем, художник добивается глубины изображения, ибо и в действительности человеческий глаз видит так, что далекие предметы кажутся ему меньше, чем близкие. Прибегают художники и к другому оптическому эффекту: краски более далеких предметов они смягчают, делая более блеклыми по сравнению с яркими красками предметов, находящихся на переднем плане.

В своем повседневном опыте мы сталкиваемся и с другими оптическими иллюзиями. Солнце и Луна вблизи горизонта выглядят по размерам больше, чем когда они стоят высоко в небе: вблизи горизонта оба светила кажутся нам ближе, и мы подсознательно поддаемся этой иллюзии. Разумеется, точные измерения показывают, что размеры Солнца и Луны остаются неизменными.

Измерив угол, под которым глаз видит диаметр Луны, мы обнаружили бы, что он близок к половине градуса. Так как половина дуги небосвода составляет 180°, угол, под которым виден диаметр Луны, равен 1/360 угловых размеров небосвода. Площадь же лунного диска составляет поразительно малую долю (около 1/100 000) площади небосвода, но если вспомнить, сколь великолепное зрелище являет собой наше ночное светило в полнолуние, то трудно поверить, что занимаемая им площадь столь ничтожна.

Ряд других оптических иллюзий связан с явлением рефракции, или преломления, света. Всем нам приходилось замечать, что палка, частично погруженная в воду, кажется переломленной в том месте, где она входит в воду.

С древних времен внимание людей привлекало такое проявление рефракции в воздухе как мираж. Это явление порождается совместным действием двух эффектов: разного преломления лучей света в неодинаково нагретых Солнцем (и потому имеющих различную плотность) слоях воздуха и полного внутреннего отражения. Когда нам случается в жаркий день ехать на автомобиле по длинному прямому участку гладкого ровного шоссе, то мы наблюдаем еще один мираж. Издали кажется, будто дорога впереди покрыта водой, но, подъехав ближе, мы убеждаемся, что воды нет и в помине. Чем же обусловлен такой эффект?

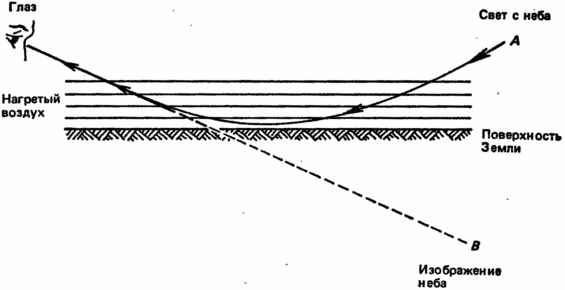
Мираж возникает только в том случае, если поверхность дороги сильно нагрета солнцем. Соприкасаясь с дорожным полотном, воздух нагревается, плотность его становится меньше, и более легкие нижние слои поднимаются вверх. Следовательно, свет в нижних слоях преломляется слабее, чем в верхних. Представим себе эту последовательность слоев с меняющейся плотностью (рис. 18). Проходя через них, свет попадает в наши глаза из нижних слоев, расположенных у самой земли. Наблюдатель видит свет, идущий в действительности из точки A,как бы приходящим из точки В.Именно такую картину он наблюдал бы, если бы перед ним простиралась водная поверхность, так как при взгляде на нее или на мокрую дорогу он увидел бы отражение неба. Таким образом, нагрев дороги создает такую же картину отражения света, какую мы привыкли связывать с водной поверхностью. Зрение вводит нас в заблуждение, и нам кажется, что дорога залита водой или что впереди расстилается водная поверхность.

Большинство приведенных нами примеров оптической иллюзии придуманы, причем намеренно, психологами. Но чтобы убедиться в постоянных ошибках зрения и понять, чем они вызваны, совсем не обязательно обращаться к искусственным примерам. Из-за рефракции света в земной атмосфере, мы продолжаем видеть Солнце и после того, как оно скрывается за горизонтом. Земля кажется нам плоской. Мы «своими глазами» видим, как Солнце обращается вокруг Земли, которая кажется нам неподвижной. Предположим, что Солнце стоит высоко в небе. На вопрос «Видите ли вы сейчас Солнце?» вы, не задумываясь, отвечаете утвердительно. Между тем испускаемый Солнцем свет доходит до нас только через восемь минут, а за это время может произойти немало событий (например, Солнце может взорваться). Когда Солнце стоит у самого горизонта, мы видим его не круглым, а несколько сплюснутым: вертикальный диаметр Солнца кажется нам несколько укороченным. Это явление также обусловлено преломлением солнечных лучей в атмосфере. Звезды же, находящиеся от нас на невообразимо больших расстояниях, кажутся нам крохотными пятнышками света.

Искажения видимых изображений часто называют иллюзиями, но «иллюзии» необычайно многообразны. Сигналы о цветовых ощущениях поступают в мозг от сетчатки глаза по трем каналам. Существуют три типа цветовых рецепторов (колбочек), каждый из них чувствителен к одному из трех первичных цветов: красному, зеленому или синему. Белый свет возбуждает все три цветовых канала. Каждый предмет поглощает одни световые лучи и отражает другие. Видимый нами цвет — это то, что предмет отражает. Белый предмет отражает падающий на него свет во всем спектре. Но является ли коричневый стол в действительности коричневым? Пламя свечи в ярко освещенной комнате выглядит тусклым, а в темной комнате — ярким. Кусок дерева кажется нам твердым, а в действительности представляет собой весьма рыхлую структуру из атомов, удерживаемых силами межатомного сцепления. Твердость куска дерева — это не твердость сплошной среды.