Даже сейчас биологи стараются по возможности не прибегать к математике. Умы же математического склада больше склоняются к физике, нежели к биологии или общественным наукам. Мэй был исключением из правила. Первоначально его интересы лежали в области абстрактных проблем устойчивости и сложности. Он пытался математически обосновать взаимозависимость этих явлений, существующих в противоборстве и неразрывной связи. Однако вскоре Мэй заинтересовался, казалось бы, несложными вопросами экологии, связанными с поведением отдельных популяций во времени. Невероятно простые модели представлялись ему неизбежным компромиссом. К тому времени, когда Мэй окончательно обосновался на одном из факультетов Принстона (в будущем австралиец станет фактически проректором по науке), он провел уже не один час, изучая варианты логистического разностного уравнения с применением математического анализа и примитивного карманного калькулятора.

Как-то, еще в Сиднее, он написал на доске в коридоре уравнение, чтобы над ним подумали студенты-выпускники. Однако уравнение зацепило его самого. «Господи, что же происходит, когда ламбда начинает превосходить точку аккумуляции?» — с напряжением размышлял Мэй. Он пытался уловить, что случается в момент приближения колебаний коэффициента роста к критической точке и превышении ее. Подставляя различные значения этого нелинейного параметра, Мэй обнаружил, что возможны коренные перемены в самой сущности системы: увеличение параметра означало возрастание степени нелинейности, что, в свою очередь, изменяло не только количественные, но и качественные характеристики результата. Подобная операция влияла как на конечное значение численности популяции, находившейся в равновесии, так и на ее способность вообще достигнуть последнего.

Когда задавалось низкое значение параметра, простая модель Мэя демонстрировала устойчивое состояние. При высоком же значении система как бы распадалась на два фрагмента и численность популяции начинала колебаться между двумя величинами. Наконец, при чрезмерном увеличении параметра поведение той же системыстановилось непредсказуемым. Но почему? Что происходило на границах различных типов ее поведения? Мэй, как и его выпускники, не мог этого уяснить.

Он рассмотрел простейшее уравнение, причем его компьютерная программа была аналогом программы Смэйла, а сам ученый пытался рассматривать объект целиком— не локально, а глобально. Уравнение было проще всего, что когда-либо изучал Смэйл. Казалось невероятным, что потенциал такой несложной задачи в генерировании порядка и беспорядка неистощим. На самом же деле программа Мэя стала лишь началом. Он рассмотрел сотни значений параметра, задействовав обратную связь и наблюдая, где именно ряд чисел придет к фиксированному значению и случится ли подобное вообще. Он сосредоточивал все больше внимания на рубеже перехода от стабильного состояния к колебательному. Используя уравнение x _c= rx(1- x), Мэй увеличивал значение параметра так медленно, как только мог. Если это значение составляло 2,7, численность популяции равнялась 0,6292. По мере увеличения параметра конечный результат так же медленно увеличивался, образуя на графике кривую, плавно поднимавшуюся слева направо.

Неожиданно, когда значение параметра превысило 3, линия раздвоилась. Численность воображаемой стаи рыб в предыдущий и последующий годы колебалась между двумя точками, не являясь единой величиной. Начиная с меньшего числа, она возрастала, а затем беспорядочно варьировалась до появления устойчивых отклонений в ту и другую стороны. Рост «холмика» на графике — небольшое увеличение параметра — вновь расщеплял колебания, генерируя ряд чисел, приходивших, в конечном счете, к четырем различным значениям, каждое из которых повторялось с регулярностью раз в четыре года [4]. Теперь компьютерная популяция Мэя увеличивалась и убывала в устойчивом четырехлетнем режиме. Длительность цикла вновь выросла в два раза — сначала с одного года до двух, затем — до четырех. И вновь подобное «круговое» поведение в итоге обнаружило стабильность: какова бы ни была начальная численность популяции, изменения ее укладывались в рамки четырехлетнего цикла.

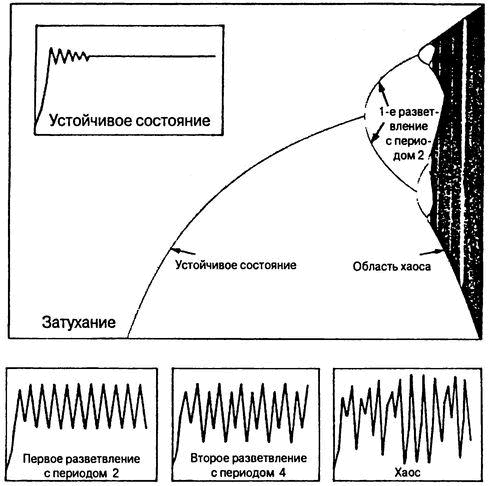
^{Рис. 3.2. Удвоение периодов и хаос. Вместо применения отдельных диаграмм для демонстрации изменений в популяциях с различной степенью воспроизводства Роберт Мэй, наряду с другими учеными, использовал так называемую разветвленную диаграмму, чтобы соединить все данные в одном изображении. На диаграмме показано, каким образом изменение одного параметра, в данном случае — способности живущей в естественных условиях популяции к снижению и увеличению числа составляющих ее особей, повлияет на поведение рассматриваемой простой системы в целом. Значения параметра откладывались слева направо по горизонтальной оси; значения конечной численности популяции — по вертикальной. В известном смысле рост значения параметра знаменует перегрузку системы, увеличение в ней нелинейного элемента. Когда это значение невелико (слева), популяция угасает. По мере его роста (в центре)популяция достигает равновесия. Затем, при дальнейшем увеличении параметра, равновесное состояние расщепляется на две ветви, подобно тому как в процессе конвекции дальнейшее нагревание жидкости делает ее нестабильной. Начинаются колебания численности популяции между двумя различными уровнями. Расщепления, или разветвления, происходят все быстрее и быстрее. Далее система становится хаотичной (справа), и численность особей может приобретать бесконечное множество значений.}

Построение графика — единственное, что позволяет обнаружить в указанных результатах хоть какой-то смысл и представить их наглядно. Мэй сделал предварительный набросок, чтобы охватить все типы поведения системы при различных параметрах. Для значений параметра, возраставших слева направо, была выбрана горизонтальная ось, для численности популяции отводилась вертикальная. Каждое из значений параметра было представлено точкой, обозначавшей конечный результат после достижения системой равновесия. Слева, там, где значения еще были небольшими, результат являл собой лишь точку. Таким образом, изменения параметра отобразились в виде линии, поднимавшейся слева направо. Когда значение параметра миновало первый критический рубеж, Мэю пришлось вычертить кривую для двух популяций, поскольку линия раздвоилась, образовав искривленную букву Y или подобие вил. Такое расщепление соответствовало переходу популяции от однолетнего цикла к двухлетнему.

По мере дальнейшего роста значения параметра количество точек удваивалось вновь и вновь, что просто ошеломляло ученого, поскольку столь сложное поведение таило в себе обманчивую устойчивость. Мэй назвал наблюдаемый феномен «змеей в джунглях математики». Раздвоения на графике изображались разветвлениями основной линии, и каждое из этих разветвлений означало, что повторяющийся образец далее вновь разделится на части. Популяция, ранее характеризовавшаяся стабильностью, колебалась между двумя различными уровнями каждый второй год. Популяция, менявшаяся в течение двухлетнего цикла, изменялась теперь в течение третьего и четвертого годов, переходя, таким образом, к четырехлетнему периоду.

Подобные разветвления наблюдались на графике все чаще и чаще — 4, 8, 16, 32… — и вдруг внезапно прекратились. После определенной точки аккумуляции периодичность уступала место хаосу, колебаниям, которые никогда не затухали, и поэтому целые зоны на графике были полностью затушеваны. Наблюдая за популяцией животных, описанной этим простейшим уравнением, можно посчитать происходящие год за годом перемены совершенно случайными, привнесенными извне. Тем не менее в самой гуще подобной беспорядочности вновь появляются стабильные циклы. Так, с возрастанием параметра неожиданно обозначается просвет с правильным, хотя и странным периодом, вроде 3 или 7. Модель меняющейся популяции повторяла саму себя в течение трехлетнего или семилетнего цикла. Затем снова, в более высоком темпе, начинались разветвления, которые удваивали период, быстро минуя новые циклы (3, 6, 12… или 7, 14, 28…) и вновь обрываясь с рождением нового хаоса.