Между прочим, вспомните, что, летая самолетом, вы, быть может, замечали, как смещаются вверх-вниз кончики его крыла. Конструктор, проектируя крыло, наделил его такими свойствами. Вероятно, вам уже ясно, что смещения, будь они малыми или большими, создают силы сопротивления. Эти силы определяют жесткость твердого тела, его способность сопротивляться внешним нагрузкам. Другими словами, в твердом теле возникают именно такие смещения, которые как раз достаточны, чтобы уравновесить приложенные внешние нагрузки. Это происходит совершенно автоматически.
Как же возникают эти силы? Дело в том, что в любом теле атомы химически связаны между собой (Приложение I). Эти связи условно можно представить в виде пружинок, хотя, конечно, ничего "твердого" в обычном вульгарном смысле этого слова в промежутках между атомами не существует (рис. 1). Те же силы, которые делают тело твердым, определяют и его химические свойства. Разрушение химических связей освобождает энергию пороха и бензина, те же связи делают резину и сталь упругими и прочными.
Рис. 1. Наглядная модель химических связей в твердом теле
Когда твердое тело полностью свободно от механических нагрузок (что бывает, строго говоря, очень редко), химические связи, или пружины в нашей модели, находятся в нейтральном положении (рис. 1, а). Любая попытка сблизить атомы (это мы называем сжатием) или оттянуть их друг от друга (что обычно называется растяжением) сопровождается небольшим укорочением (рис. 1, б) или удлинением (рис. 1, в) межатомных пружин во всем объеме материала. При этом ядра атомов считаются жесткими, кроме того, в твердом теле атомы обычно не обмениваются местами, по крайней мере при умеренных, или "безопасных", нагрузках. Таким образом, податливость твердого тела определяется межатомными связями. Жесткость этих связей может изменяться в широких пределах, но для большинства веществ она намного выше, чем у тех металлических пружин, с которыми мы встречаемся в повседневной жизни. Очень часто величины межатомных сил весьма и весьма велики. Этого и следовало ожидать, если вспомнить о силах, которые могут быть получены при разрыве химических связей горючих или взрывчатых веществ.
Хотя абсолютно жестких тел, то есть таких, которые под действием внешних сил совершенно не изменяют своей формы, в природе не бывает, смещения во многих предметах часто оказываются очень малыми. Например, если я наступлю на обычный строительный кирпич, то его высота уменьшится примерно на 1/20000 см. А два любых соседних атома в кирпиче станут ближе один к другому на расстояние ~1/500000A (2·10-14 см). Величина эта невероятно мала, но она соответствует совершенно реальным перемещениям атомов. Конечно, в крупных конструкциях перемещения элементов не всегда малы. Канаты, на которых висит мост через залив Форт (Шотландия), все время растянуты примерно на 0,1%, что при их общей длине почти 3 км составляет около 3 м. В этом случае атомы железа, расстояние между которыми в не нагруженном состоянии около 2 А, удаляются на величину ~2/1000 А.
Тот факт, что расстояние между атомами действительно изменяется под нагрузкой, был многократно про верен путем постановки самых различных экспериментов. Наиболее наглядные результаты дает стандартный метод измерения межатомных расстояний по отклонению пучка рентгеновских лучей при прохождении его через кристалл, основанный на явлении дифракции. Более чем полувековая практика позволила довести этот метод до весьма высокой точности. Опыты показали, что смещения атомов в металлах, например, строго пропорциональны величине, на которую удлиняется (или укорачивается) весь кусок металла. В этих экспериментах наблюдались изменения межатомных расстояний примерно до 1%. На рис. 2 показаны результаты измерений на мягкой стали, в которой максимальные смещения атомов были около 0,5%.
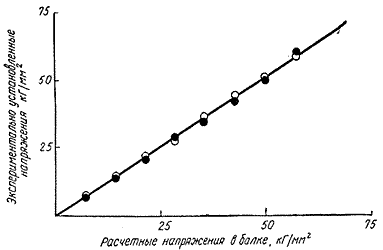
Рис. 2. Сравнение напряжений, установленных экспериментально с помощью дифракции рентгеновских лучей (методом двух экспозиций), с расчетными напряжениями, вычисленными по кривизне изогнутой балки (отожженная малоуглеродистая сталь). Белый кружок - данные экспериментатора A, черный - экспериментаторов B и C.
(обратно)
Напряжения и деформации, что это?
Все эти рассуждения подводят нас к понятиям "напряжение" и "деформация". Когда мы говорили о силах, то имели в виду полные величины сил, действующих на тело. Такой силой мог быть любой груз. Когда мы говорили о смещении под нагрузкой, то имели в виду полные смещения независимо от размеров объекта, будь он большим или малым. Однако все это не позволяет нам сравнивать большой объект под большой нагрузкой с малым объектом под меньшей нагрузкой. Например, если из стали одного сорта изготовить крошечную деталь пишущей машинки и корпус воздушного лайнера, то какие характеристики этого материала, работающего в столь различных условиях, можно было бы сравнивать? Без ответа на этот вопрос мы не можем продолжать разговор о материалах и конструкциях. Нужные нам величины называются напряжением и деформацией. Напряжение - это нагрузка, отнесенная к единице площади, то есть σ= P/F, где σ - напряжение, Р - нагрузка, F - площадь. Приведенная формула также повседневна, как и привычные всем выражения "килограмм масла стоит 3 рубля" или "машина проходит 10 километров на одном литре бензина". Следовательно, если мы снова возьмем кирпич с поперечным сечением 25x12 см, то есть площадью сечения 300 см2, и я наступлю на него, приложив к нему силу своего веса 75 кг, то сжимающее напряжение, которое я вызову в кирпиче, будет σ = P/F = 75/300 = 0,25 кг/см2
Точно так же, если кирпичная опора моста имеет поперечное сечение 10x5 м и на мост въезжает локомотив весом в 125 т, то сжимающее напряжение в кирпичной кладке будет около 0,25 кг/см2. Теперь мы с полной определенностью можем сказать, что в обоих случаях напряжения в кирпиче примерно одинаковы, и если одна конструкция не разрушается, то, по-видимому, не разрушится и другая. Что касается кирпичей, то их молекулы поджимаются одна к другой одинаковыми силами, хотя вес локомотива и вес моего тела совершенно различны. Очевидно, что инженера должны интересовать именно такие величины.
Напряжение может быть выражено в килограммах на квадратный миллиметр (кг/мм2), килограммах на квадратный сантиметр (кг/см2), ньютонах на квадратный метр (Н/м2) или других подобных единицах[8].
Разумеется, эти единицы применяются к любым поперечным сечениям и к любой точке, а не только к квадратным миллиметрам, квадратным сантиметрам и т.п. То, что цена одного килограмма масла 3 рубля, вовсе не означает, что ее используют лишь для веса в один килограмм. Деформация - это величина удлинения стержня под нагрузкой, отнесенная к начальной длине. Очевидно, что отрезки различной длины при одной и той же нагрузке получают в конструкциях различное удлинение. Если обозначить деформацию через ε, то ε = Δl / l
где Δl — полное удлинение, а l — начальная длина. Так что, если стержень длиною 100 см под нагрузкой удлиняется на 1 см, его деформация будет 1/100, или 1%. Такая же деформация будет у стержня длиной 50 см, растянутого на 1/2 см, и т.д. При этом толщина стержня роли не играет, не важно также, что вызвало удлинение.
В данном случае нас интересует лишь то, насколько изменилось взаимное положение атомов и молекул. Деформация, так же как и напряжение, не зависит от размера образца. Деформация есть отношение удлинения к начальной длине, и, следовательно, она безразмерна и не зависит от того, какой системой единиц мы пользуемся.
(обратно)