Пфальц (Pfalz), средневековое княжество на Ю.-З. Германии. Известно с 12 в., когда владетели П. закрепили за собой титул и права пфальцграфов и стали именоваться пфальцграфами Рейнскими (по месту расположения территории княжества). В 1214 П. перешёл к роду баварских Виттельсбахов. В 1329 отделился от Баварии под властью особой ветви Виттельсбахов; к нему отошла также северная часть Баварии, которая в отличие от Рейнского, или Нижнего, получила название Верхний П. В 1356 пфальцграфы Рейнские получили права курфюрстов. В 1386 в их резиденции Гейдельберге был основан первый в Германии университет. Во время Реформации П. — оплот кальвинизма (со 2-й половины 16 в.). Курфюрст П. Фридрих V, возглавлявший Протестантскую унию германских князей, в 1619 был избран королём Чехии, но в ходе Тридцатилетней войны 1618—48 после поражения чешских войск в 1620 у Белой Горы потерял Чехию, а в 1623 и П., который был передан Баварии. По Вестфальскому миру 1648 курфюршество П. (но без Верхнего П.) было восстановлено. В 1793—94 часть Рейнского П. была занята французскими войсками и в 1801 присоединена к Франции, другая часть поделена между германскими княжествами. В 1814—15 большая часть П. отошла к Баварии, меньшая была разделена между Пруссией, Баденом и Гессен-Дармштадтом.

Пфа'льцграф (нем. Pfaizgraf, буквально — дворцовый граф), во Франкском государстве придворный королевский служащий, председательствовавший в дворцовом суде (при Каролингах занял высокое положение, суд П. обособился от королевского). В Германии 9—11 вв. П., как и граф округа, считался формально королевским должностным лицом, но со временем превратился во владетельного князя. Особенно высокое положение занял П. Рейнский (князь Пфальца). Титул П. был отменен в 1806.

Пфа'льцский лес (Pfalzer Wald), горы на З. ФРГ, по левобережью р. Рейн, между Вогезами на Ю. и Рейнскими Сланцевыми горами на С. Длина около 100 км, высота до 687 м (гора Доннерсберг). Восточная, наиболее высокая часть П. Л. (Хардт), круто обрывается к Верхнерейнской низменности. Сложены преимущественно пестроцветными песчаниками, образующими причудливые формы выветривания. Состоят из нескольких ступенчато понижающихся к З. плоскогорий, глубоко расчленённых притоками Рейна. Широколиственные и сосновые леса, местами верещатники. В П. Л. — одноимённый природный парк.

Пфа'льцское насле'дство, Война за Пфальцское наследство, Орлеанская война, велась в 1688—97 между Францией и коалицией европейских государств — так называемой Аугсбургской лигой. Началась в сентябре 1688 с вторжения в Пфальц французских войск Людовика XIV, который выступил с притязаниями на значительную часть территории Пфальцапод предлогом защиты прав жены своего брата герцогини Орлеанской (дочери умершего в 1685 курфюрста Карла Пфальцского). Военные действия распространились и на др. районы Германии, на Нидерланды, Испанию; французские войска были посланы также в Ирландию для поддержки антианглийского восстания 1688—91; война шла и на море (вплоть до берегов Америки). Французская армия, подвергшая опустошению Пфальц, одержала ряд крупных побед на суше (при Флёрюсе 1 июля 1690, у Стенкеркена 3 августа 1692, у Нервиндена 29 июля 1693), но потерпела поражение от англо-голландского союзного флота у мыса Аг 29 мая 1692. Война закончилась Рисвикским миром 1697.

Пфафф (Pfaff) Иоганн Фридрих (22.12.1765, Штутгарт, — 21.4.1825, Галле), немецкий математик, член Берлинской АН (1817). Профессор математики университетов в Хельмштедте (1788—1810) и Галле (с 1810). П. принадлежат исследования по уравнениям в дифференциалах (так называемые Пфаффа уравнения).

  Соч.: Allgemeine Methode partielle Differentialgleichungen zu integrieren (1815), Lpz., 1902.

  Лит.: Kowalewski G. W. H., Grosse Mathematiker. Eine Wanderung durch die Geschichte der Mathematik, B. 1938, S. 228—47.

Пфа'ффа уравне'ния, уравнения вида

X₁dx₁ + X₂dx₂ + ... + X_ndx_n = ,     (1)

где X₁, X₂, ..., X_n — заданные функции независимых переменных x₁, x₂, ..., x_n. Изучались И. Ф. Пфаффом (1814—15). Решение уравнения (1) состоит из соотношений

таких, что уравнение (1) является следствием их и соотношений df₁ = 0, df₂ = 0, ..., df_m= 0. Соотношения (2) определяют интегральное многообразие П. у. (1). Если через каждую точку n-мерного пространства x₁, x₂, ..., x_nпроходит (n — 1)-мерная интегральная гиперповерхность, т. е. если уравнение (1) интегрируется одним соотношением, содержащим одну произвольную постоянную, то оно называется вполне интегрируемым.

  В случае трёх независимых переменных х, у, z П. у. может быть записано в виде

Pdx + Qdy + Rdz = 0,     (1’)

где Р = Р (х, у, z), Q = Q (х, у, z), R = R (х, у, z). Геометрически решение уравнения (1’) означает нахождение кривых в пространстве х, у, z, ортогональных в каждой своей точке векторному полю {Р, Q, R}, т. е. таких кривых, нормальная плоскость к которым в каждой точке содержит вектор поля. Такие кривые являются интегральными кривыми уравнения (1’). Если задать одно соотношение Ф (х, у, z) = 0 произвольно, т. е. искать интегральные кривые на произвольной гладкой поверхности, то из уравнения (1’) и соотношения

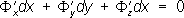
находятся, например, dy/dx и dz/dx как функции х, у, z, и задача сводится к интегрированию системы двух обыкновенных дифференциальных уравнений первого порядка. Решая ее, находят двупараметрическое семейство кривых, из которого выделяют однопараметрическое семейство интегральных кривых уравнения (1'), лежащих на заданной поверхности Ф (х, у, z) = 0. Это семейство интегральных кривых может рассматриваться как пересечение заданной поверхности и однопараметрического семейства поверхностей Ф₁(х, у, z, с) = 0, т. е. общее решение П. у. (1') состоит из двух соотношений Ф (х, у, z) = 0 и Ф₁(х, у, z, с) = 0, из которых первое произвольно, а второе определяется по первому. П. у. (1') интегрируется одним соотношением F (х, у, z, с) = 0, т. е. является вполне интегрируемым, если выполняется условие интегрируемости

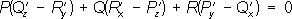
тождественно относительно х, у, z. Геометрически это значит, что существует однопараметрическое семейство интегральных поверхностей П. у. (1’), ортогональных в каждой точке векторному полю {Р, Q, R}. Любая кривая на интегральной поверхности является интегральной кривой П. у. (1’).