большое – малое длинное – короткое широкое – узкое толстое – тонкое.

Далее следуют некоторые связанные с этим или случайные вещи, которые также изменяют фигуру, как, например:

молодое – старое жирное – тощее красивое – безобразное жесткое – мягкое.

Далее употребляются также и другие понятия, которые служат для подобных же изменений, как, например:

кривое – прямое ровное – неровное высокое – низкое круглое – угловатое острое – тупое.

Далее, изменения вызывают также следующие понятия: отвесное, поперечное, косое.

Также вызывают изменения:

добавлять – убавлять много – мало.

Далее пользуются [понятиями]:

правый – левый спереди – сзади сверху – снизу.

С помощью вышеназванных вещей можно отличить всякую вещь от ранее сделанной, расчленить по-иному и сделать иною, чем раньше.

Покажем это немного на деле и возьмем сначала два понятия – большое и малое. Их следует применять во всех вещах, которые хотят сделать большими или малыми. Сами по себе они не придают фигуре иного изменения, кроме того, что скажут: эта большая или это маленькая вещь, причем обе эти вещи могут быть одного рода и одинаковых пропорций. Поэтому названные размеры могут быть сделаны большими или малыми, и каждая часть будет выражена в своей мере и числе. Возьмем для примера маленький домик, подле которого строят или воздвигают большой дворец, или отношение маленького шара к большому. Итак, как сказано выше, понятия большое и малое не изменяют фигуры.

Для того же, чтобы понятия большое и малое внесли в фигуры изменения, которые создали бы различие в них, понятия эти следует применять не во всем сразу, но лишь в отдельных частях. Если увеличить одни части и уменьшить другие, вид вещи станет иным, как, например, если ты увеличишь фигуру выше пояса и уменьшишь ее ниже пояса или наоборот. Применяя это во всех членах, как в наименьших, так и в наибольших, и в каждой части особо, можно получить бесконечное множество изменений. При этом следует заметить, что ни одна вещь не будет признана большой или малой по отношению к другой, если рядом с большим или малым не будет помещена его противоположность. И каждый может пользоваться этим по мере надобности.

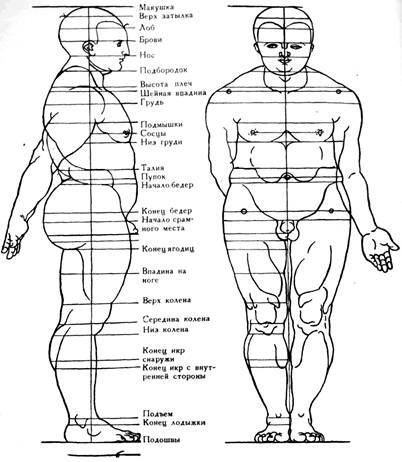
Возьмем далее понятия длинное и короткое. Сделаем, исходя из них, длинным или коротким первого толстого человека, описанного в первой книжечке. И заметь теперь, что если человек этот будет удлинен, он станет тоньше и уже во всех своих пропорциях; если же он будет укорочен, он станет толще и шире в пропорциях и сложении, ибо при подобном удлинении и укорачивании толщину и ширину оставляют во всех частях неизменными, как они указаны для первого описанного мужчины. И если привести обоих мужчин – удлиненного и укороченного – снова к длине первого описанного мужчины, то все их размеры в толщину и в ширину станут иными, нежели у первого описанного мужчины, и они будут выглядеть неодинаково друг с другом, потому что один стал тоньше и уже, а другой толще и шире. Известен также способ, благодаря которому можно удлинять или укорачивать пропорционально друг другу меры всех членов между всеми поперечными линиями, показывающими размеры всех частей тела в длину. Если расставить их далеко друг от друга, то изображение удлинится; если же сблизить их, то изображение станет короче. И если, как говорилось выше, ничего при этом не прибавлять и ничего не отнимать во всех размерах членов в толщину и ширину, тогда понятия длинное и короткое вызовут изменения в фигурах. И если снова измерить последние циркулем, описание их будет иным, нежели первого мужчины. Но было бы весьма затруднительно, если бы всякий раз, укорачивая или удлиняя фигуру, надо было бы тратить много труда, находя с помощью циркуля каждую часть, поэтому я покажу сейчас способ, который позволит быстро и легко достигнуть такого удлинения или сокращения.

Сначала я должен иметь размеченную точками линию, пропорционально которой я размечу затем точками две другие – длинную и короткую. Сделаем это так. Я беру линию, равную длине первого описанного мужчины первой книжечки; пусть она будет ab. Эта линия разделена точками, образованными проходящими через все концы членов поперечными линиями, при помощи которых была описана фигура. Я ставлю линию аbотвесно и помещаю в стороне вдали от нее точку с. Из этой точки я провожу через все точки отвесной линии оbпрямые линии и веду их дальше. Когда образуется треугольник abcи проведенные линии будут выглядеть похожими на щетку, тогда я проведу рядом с отвесной линией аbдве другие отвесные парные линии, по одной с каждой стороны: более короткую ближе к точке с, ее я обозначу вверху d, a внизу е; более же длинную я проведу снаружи, она пусть будет вверху f, а внизу g. И чем длиннее я хочу сделать мужчину, тем дальше наружу я помещаю линию, а чем короче он должен быть, тем ближе я придвигаю линию к точке с. Таким образом, мы достигли искомого деления с помощью прямых линий из точки с, проходящих через три отвесные линии ab, deи fg, и каждая линия разделена в полном соответствии с другими.

Этот указанный выше способ я изобразил здесь не только для такого употребления, но и для того, чтобы пользоваться им в дальнейшем. И я дал этой фигуре свое наименование и называю ее изменителем, потому что каждая вещь изменяется при ее помощи. И действие этого изменителя распространяется на два понятия – большое и малое.

С помощью такого изменителя каждая вещь, имеющая бесконечное число частей, может быть превращена в большую или меньшую такой же формы. И из этого можно сделать много удивительных вещей. С помощью такого изменителя можно придать фигуре, первоначально имевшей длину в семь голов, длину в восемь, девять – до десяти голов, если прибавлять длину головы один, два, три раза к расстоянию между головой и подъемом ступни. Но если фигура будет настолько изменена, следует тотчас же удлинить немного, в меру необходимости, голову, чтобы она не казалась слишком малой. Но тогда фигура не будет больше содержать в своей длине столько голов, как раньше.

И в особенности следует иметь в виду, что, изменяя с помощью изменителя размеры отдельно описанных в первой книжечке кисти руки и ступни, надо работать очень внимательно.

Когда эти обе вновь проведенные линии – длинная fgи короткая de– размечены точками и каждая из них пересечена поперечными линиями во всех полученных точках, тогда я рисую длинную и короткую фигуру мужчины сбоку и спереди по тем размерам в толщину и в ширину, которые указаны в первой книжечке. И я нарисовал удлиненного и укороченного мужчину, какими они должны быть, по найденным этим способом размерам в длину. Но не имея возможности из-за небольшого размера бумаги напечатать здесь фигуру удлиненного мужчины более высокой, я снова привел их все к первоначальной длине и нарисовал по вновь найденным мерам…[128]

Исходя из понятий длинное и короткое я хочу теперь снова вернуться к описанной в первой книжечке мужской голове, которая разделена перпендикулярными перекрещивающимися линиями и заключена в куб или форму наподобие игральной кости,[129] и хочу теперь показать, как можно вытянуть, т. е. повысить или приплюснуть этот куб и как при этом узнать, насколько он станет тоньше и уже при таком же объеме, если он будет вытянут, и насколько он станет толще и шире, если его приплюснуть. Для этого надлежит поступить следующим образом.

Я возьму правильный квадратный в основании куб, одинаковый со всех сторон, такой же высоты, как вышеназванная голова, ибо она должна быть представлена заключенной в этом кубе. И сначала, прежде чем что-либо будет описано или обозначено в нем внутри, я буду иметь дело только с кубом или игральной костью. И пусть каждый выберет сам, насколько он повысит, вытянет или приплюснет куб…[130]